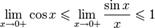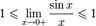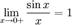Свойства пределов.бесконечно больш и малые.Свойства бесконечно малых и бесконечно больших величин и связь между ними
Пусть f 1 (x) и f 2 (x) бесконечно малые величины при 1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая:
2. Произведение бесконечно малых величин есть величина бесконечно малая:
3. Произведение бесконечно малой величины на константу С или на функцию, имеющую конечный предел
Пусть 1. Сумма бесконечно больших величин есть величина бесконечно большая:
2. Произведение бесконечно больших величин есть величина бесконечно большая:
3. Произведение бесконечно большой величины на константу С, или на функцию, имеющую конечный предел
41.замечательные пределы. Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны: Первый замечательный предел:
(из Подставляя в (1), получим:
Так как при
Найдём левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
|

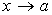 ,
,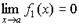 и
и 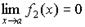 .
.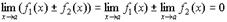 . (4.17)
. (4.17)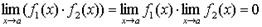 . (4.18)
. (4.18)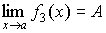 , есть величина бесконечно малая:
, есть величина бесконечно малая: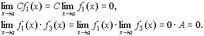 . (4.19)
. (4.19)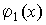 и
и 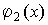 бесконечно большие величины при
бесконечно большие величины при  и
и 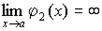 .
.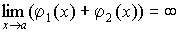 .
.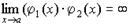 . (4.21)
. (4.21)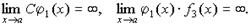
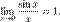 Второй замечательный предел:
Второй замечательный предел: 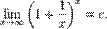 Первый замечательный предел
Первый замечательный предел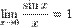 Доказательство
Доказательство 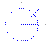 Рассмотрим односторонние пределы
Рассмотрим односторонние пределы 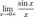 и
и 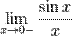 и докажем, что они равны 1.Пусть
и докажем, что они равны 1.Пусть 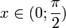 . Отложим этот угол на единичной окружности (
. Отложим этот угол на единичной окружности ( ).Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке
).Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке 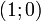 . Точка H — проекция точки K на ось OX. Очевидно, то:
. Точка H — проекция точки K на ось OX. Очевидно, то: 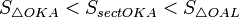 (1)(где
(1)(где 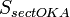 — площадь сектора
— площадь сектора 
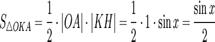
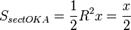
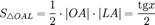
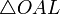 :
: 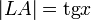 )
)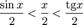
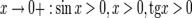 :
: 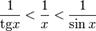 Умножаем на
Умножаем на 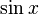 :
: 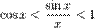 Перейдём к пределу:
Перейдём к пределу: