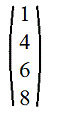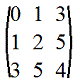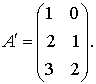Матрица. Виды матриц. Сложение и вычитание матриц, умножение на число, транспонирование. Примеры.

Матрицей называется прямоугольная таблица чисел. Так, 230

104 есть матрица с двумя строками и тремя столбцами. Обозначим ее A. Обычно элементы матрицы обозначаются теми же буквами, что и матрица, но строчными: A = (ai j). В этой матрице всего 6 элементов: a 11 = 2, a 12 = 3, a 13 = 0, a 21 = 1, a 22 = 0, a 23 = 4 (надо читать эти элементы так: a 11 — а-один-один, a 12 — а-один-два и т.д.). Число строк и число столбцов в матрице называются ее размерами, причем число строк называют первым. Итак, A есть матрица размером 2 × 3. Две матрицы считаются равными (одинаковыми) тогда и только тогда, если у них совпадают их размеры, т.е. число строк и число столбцов, и совпадают сами строки и столбцы. Пусть, например, A = (ai j) есть матрица m × n и B = (bi j) есть матрица k × s; тогда A = B, если и только если k = m, s = n и ai j = bi j для любых i = 1,..., m и j = 1,..., n. Таким образом, бессмысленно говорить о равенстве матриц при несовпадении их размеров. Если число строк равно числу столбцов, то матрица называется квадратной. В квадратной матрице элементы ai i образуют главную диагональ матрицы. Если в квадратной матрице все элементы — нули и только на главной диагонали все элементы есть единицы, то такая матрица называется единичной. Так,

E 3 = 100

001 есть единичная матрица размера 3. В каждой размерности есть своя единичная матрица.Рассмотрим матрицу A размерами m × n. Каждую ее строку мож- но считать вектором-строкой размерности n и каждый столбец — вектором-столбцом размерности m. Обозначим i- ю строку-вектор a i, j- й столбец-вектор Aj, тогда матрицу A можно представить упо- рядоченным набором векторов-строк:

A = a 1

.

.

.

a m или упорядоченным набором векторов-столбцов: A = (A 1,..., An). Заметим, что векторы можно рассматривать как частный случай матриц. Так, вектор-строка может рассматриваться как матрица содной строкой; аналогично вектор-столбец — как матрица с одним столбцом.

Виды матриц

1. Прямоугольные: m и n - произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7) - во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и aij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: aij=0, i=1,2,...,m

j=1,2,...,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

9. Симме трическая матрица: m=n и aij=aji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A'=AНапример,

10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем aii=-aii) Пример.

11. Эрмитова матрица: m=n и aii=-ãii (ãji - комплексно - сопряженное к aji, т.е. если A=3+2i, то комплексно - сопряженное Ã=3-2i) Пример

Сложение матриц - поэлементная операция

Вычитание матриц - поэлементная операция

Умножение матрицы на число

В результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на число.

Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число. Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы

Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.

Пример 1. Составить транспонированную матрицу, полученную из А:

Решение: Поменяем местами строки и столбцы, сохраняя порядок:

Операция умножения матриц

Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

A×B = C;

Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

Свойства операции умножения матриц.

1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

Перестановочными могут быть только квадратные матрицы одного и того же порядка. А×Е = Е×А = А

Очевидно, что для любых матриц выполняются следующее свойство: A×O = O; O×A = O, где О – нулевая матрица.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:(АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно: А(В + С) = АВ + АС (А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа a верно соотношение: a(AB) = (aA)B = A(aB).

5) Если определено произведение АВ, то определено произведение ВТАТ и выполняется равенство: (АВ)Т = ВТАТ, где

индексом Т обозначается транспонированная матрица.

6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB.