ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Определение. Вероятность события А, найденная в предположении, что событие В наступило, называется условной вероятностью события А относительно события В. Обозначать ее будем символом РВ(А). В таком случае РВ(А) означает вероятность события А, вычисленную в предположении, что событие В не наступило. Пример. С первого станка на сборку поступило 200 деталей, из которых 180 годных, со второго — 300, из которых 260 годных. Найти вероятность события А, состоящего в том, что взятая наудачу деталь будет годной, и условные вероятности его относительно событий В и Решение. Вероятность события А равна отношению числа всех годных к общему числу изготовленных на обоих станках деталей: Р (А) =(180+260)/(200+300)=0.88. Условная вероятность события А относительно события В (вероятность того, что взятая наудачу деталь годная, если известно, что она изготовлена на первом станке) РВ(А) = 180/200 = 0,9. Условная вероятность события А относительно события В, т. е. вероятность того, что взятая деталь годная, если известно, что она изготовлена не на первом (на втором) станке, Теорема (умножения вероятностей). Вероятность произведения событий А и В равна произведению вероятности одного из них на условную вероятность другого относительно взятого первым, т. е.Р (АВ) = Р (А) • РА (В) или Р (AB)= Р (В) • РВ (А). Задача. Среди 25 электрических лампочек четыре нестандартные. Найти вероятность того, что две взятые одновременно лампочки окажутся нестандартными. Решение. Искомое событие состоит в том, что нестандартными будут и первая (событие А) и вторая (событие В) лампочки. Но Р(А) = 4/25, а РА (В) = 3/24, так как при наступлении события А общее число лампочек и число нестандартных среди них по сравнению с первоначальным уменьшится на одну. Таким образом, Р (АВ) = 4/25*3/24=0,02. Задача. На станции отправления имеется 8 заказов на отправку товара: пять – внутри страны, а три – на экспорт. Какова вероятность того, что два выбранных наугад заказа окажутся предназначенными для потребления внутри страны. Решение. Событие А – первый взятый наугад заказ, В – соответственно второй, P (АВ) = 5/8*4/7=20/56. Определение. Событие А будем называется зависимым от события В, если вероятность события А меняется при наступлении события В. Совершенно естественно называть событие А независимым от события В, если вероятность события А не изменяется при наступлении события В. Следовательно, если событие А независимо от события В, то Однако независимость и зависимость событий обладают свойством взаимности, а именно справедлива теорема: Теорема. Если событие А независимо от события В, то и В независимо от А. Если же событие А зависимо от события В, то и событие В зависимо от А. Определение. События А и В называются независимыми, если вероятность одного из них не изменяется при наступлении другого. В противном случае события А и В называются зависимыми. Независимость более чем двух событий может быть различной. Определение. События А, В, С,...., К называются попарно независимыми, если независимы между собой любые два из них. Определение. События А, В, С,..., К называются независимыми в совокупности, если вероятность каждого из них не меняется при наступлении других событий (одного или нескольких в любой комбинации и в любом числе). Независимость событий в совокупности является более сильным требованием, чем их попарная независимость. Теорема умножения вероятностей для двух независимых событий имеет более простой вид. Теорема. Вероятность произведения двух независимых событий равна произведению их вероятностей: Задача. Считая вероятность безотказной работы станка в течение смены равной 0,9, найти вероятность безотказной работы двух станков в течение смены. Решение. Считая события А и В, состоящие в безотказной работе в течение смены соответственно первого и второго станков, независимыми и применяя к ним теорему умножения вероятностей получим: Р (АВ) = 0,9 • 0,9 =*0,81. Теорему умножения вероятностей легко обобщить на любое конечное число событий. Теорема. Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих каждому из них событий, т. е.Р (АВС...КL) = Р(А) • РА (В) • PAB (С)...PABC…K (L). Если события А, В, С,..., K, L независимые в совокупности, то формула упрощается, а именно: Р (АВС...КL) = Р(А) • Р (В) • P (С)... P (L). т. е. вероятность произведения конечного числа независимых в совокупности событий равна произведению их вероятностей. Задача. На десяти карточках напечатаны цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Найти вероятность того, что три наудачу взятые и поставленные в ряд карточки составят число 125. Решение. Искомое событие О произойдет, если первой будет взята карточка с цифрой 1 (событие А), вторая — с цифрой 2 (событие В), третья — с цифрой 5 (событие С). Вероятность его по теореме умножения вероятностей для трех. зависимых событий: P= 1/10*1/9*1/8=1/720=0,0014. Задача. Рабочий обслуживает четыре однотипных станка. Вероятность того, что станок (любой) в течение часа потребует внимания рабочего, равна 0,6. Предполагая, что неполадки на станках независимые, найти вероятность того, что в течение часа потребуют внимания рабочего: а) все четыре станка; б) ни один станок; в) по крайней мере один станок. Решение. а) Обозначим через А1, А2, А3, А4 события, состоящие в том, что в течение часа потребуют внимания рабочего соответственно первый, второй, третий, четвертый станки. По теореме умножения вероятностей для независимых событий вероятность того, что в течение часа все станки потребуют внимания рабочего, т. е. произойдут события все эти события, равна: P= 0,64 = 0,1296. б) Вероятность того, что в течение часа станок (любой) не потребует внимания рабочего по правилу нахождения вероятности противоположного события: в) Событие, состоящее в том, что в течение часа по крайней мере один из четырех станков потребует внимания рабочего, и событие В, рассмотренное в пункте «б», противоположные. Поэтому вероятность искомого события Задача. Студент выучил 20 вопросов из 25. Какова вероятность, что он ответит на три предложенных ему вопроса, ответит хотя бы на 1 вопрос? Решение: A-студент ответит на первый вопрос, В - студент ответит на второй вопрос, С - студент ответит на третий вопрос, тогда: P(студент ответит на все три вопроса) =
|

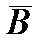 , если событие В состоит в том, что эта деталь изготовлена на первом станке.
, если событие В состоит в том, что эта деталь изготовлена на первом станке. =260/300=0.87.
=260/300=0.87. .
.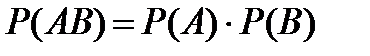
 Поэтому вероятность события В, заключающегося в том, что в течение часа ни один станок не потребует внимания рабочего, т. е. произойдут события
Поэтому вероятность события В, заключающегося в том, что в течение часа ни один станок не потребует внимания рабочего, т. е. произойдут события  : P(В)= 0,44 = 0,0256.
: P(В)= 0,44 = 0,0256. :
:  1- 0,0256 = 0,9744.
1- 0,0256 = 0,9744. . Т.е. P=20/25*19/24*18/23=57/115=0.5. D – студент ответит хотя бы на один вопрос. Противоположное событие – что не ответит ни на один вопрос. P(D) = 1-5/25*4/24*3/23=0.996.
. Т.е. P=20/25*19/24*18/23=57/115=0.5. D – студент ответит хотя бы на один вопрос. Противоположное событие – что не ответит ни на один вопрос. P(D) = 1-5/25*4/24*3/23=0.996.


