Формулы Бейеса вычисления вероятности. Примеры.
Пусть H 1, H 2,..., Hn - полная группа событий и А Ì W – некоторое событие. Тогда по формуле для условной вероятности Здесь P (Hk / A) – условная вероятность события (гипотезы) Hk или вероятность того, что Hk реализуется при условии, что событие А произошло. По теореме умножения вероятностей числитель формулы (*) можно представить в виде P Для представления знаменателя формулы (*) можно использовать формулу полной вероятности P (A) Теперь из (*) можно получить формулу, называемую формулой Байеса: По формуле Байеса исчисляется вероятность реализации гипотезы Hk при условии, что событие А произошло. Формулу Байеса еще называют формулой вероятности гипотез. Вероятность P (Hk) называют априорной вероятностью гипотезы Hk, а вероятность P (Hk / A) – апостериорной вероятностью. Пример. Рассмотрим приведенную выше задачу об электролампах, только изменим вопрос задачи. Пусть покупатель купил электролампу в этом магазине, и она оказалась бракованной. Найти вероятность того, что эта лампа изготовлена на втором заводе. Величина P (H 2) = 0,5 в данном случае это априорная вероятность события, состоящего в том, что купленная лампа изготовлена на втором заводе. Получив информацию о том, что купленная лампа бракованная, мы можем поправить нашу оценку возможности изготовления этой лампы на втором заводе, вычислив апостериорную вероятность этого события. Выпишем формулу Байеса для этого случая Задачи с решениями. 1.В первой урне 7 белых и 3 черных шара, во второй – 8 белых и 2 черных. При перевозке из первой урны во вторую урну перекатились два шара. После того, как шары во второй урне перемешались, из неё выкатился шар. Найти вероятность того, что выкатившийся из второй урны шар белый. Пусть событие Н 1 состоит в том, что из первой урны во вторую перекатились два белых шара, событие Н 2 состоит в том, что перекатились два чёрных шара, а событие Н 3 состоит в том, что перекатились шары разного цвета. Можно вычислить вероятности Р (Н 1) = Если реализовалась гипотеза Н 1, то во второй урне оказалось 10 белых и 2 черных шара. Обозначим через А событие, заключающееся в том, что из второй урны выкатился белый шар. Тогда Р (А/Н 1) = 2. В условие задачи №1 внесем изменение. Пусть после того, как из первой урны во вторую перекатились два шара и шары во второй урне перемешались, из неё выкатился белый шар. Найти вероятность того, что из первой урны во вторую перекатились разноцветные шары. Вычисления предыдущей задачи подставим в формулу Байеса Р (Н 3/ А) = Р (А / Н 3) Р (Н 3)/ Р (А) = (3/22)(7/15)/(47/33) = 7/47 3. В ящике лежат 20 теннисных мячей, в том числе 15 новых и 5 играных. Для игры выбираются 2 мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекаются ещё два мяча. Найти вероятность того, что вторая игра будет проводиться новыми мячами. Обозначим через А событие, заключающееся в том, что вторая игра будет проводиться новыми мячами. Пусть гипотеза Н 1 состоит в том, что для первой игры были выбраны два новых мяча, гипотеза Н 2 состоит в том, что для первой игры были выбраны новый и играный мячи, гипотеза Н 3 состоит в том, что для первой игры были выбраны два играных мяча. Определим вероятности гипотез: Р (Н 1) = Теперь вычислим условные вероятности события А. Р (А/Н 1) = Осталось подставить результаты вычислений в формулу полной вероятности Р (А) = 4. Сообщение со спутника на землю передаётся в виде бинарного кода, то есть как упорядоченного набора нулей и единиц. Предположим, что послание на 70% состоит из нулей. Помехи приводят к тому, что только 80% нулей и единиц правильно распознаются приёмником. Если принят сигнал “1”, то какова вероятность того, что отправлен сигнал “0”? Пусть событие В 0 состоит в том, что отправлен сигнал “0”, а событие В 1 – в том, что отправлен сигнал “1”. Пусть событие А 0 состоит в том, что принят сигнал “0”, с событие А 1 – в том, что принят сигнал “1”. Нас интересует Р (В 0/ А 1). По условию Р (В 0) = 0,7 Р (В 1) = 0,3 Р (А 0/ В 0) = 0,8 Р (А 1/ В 0) = 0,2 Р (А 1/ В 0) = 0,8 Р (А 0/ В 1) = 0,2 По формуле Байеса получаем Р (В 0/ А 1) = 0,2×0,7/(0,2×0,7+0,8×03) = 0,37. 5. Бригада, работающая в дневную смену, производит изделий в два раза больше, чем бригада, работающая в ночную смену. Отсюда следует, что если выбрать случайным образом изделие, произведённое в цеху, то с вероятностью 2/3» 0,66 оно произведено бригадой, работающей днём. Это априорная вероятность. Известно, что бригада, работающая днём, производит 3% некондиционных изделий, а бригада, работающая ночью, – 7% некондиционных изделий. Пусть случайным образом отобранное изделие оказалось некондиционным. Тогда по формуле Байеса можно вычислить апостериорную вероятность того, что это изделие произведено дневной бригадой P (Н 1/ А) = (3/100)(2/3)/((3/100)(2/3) + (7/100)(1/3))» 0,632 Как видно, апостериорная вероятность интересующего нас события здесь несколько ниже априорной вероятности.
|

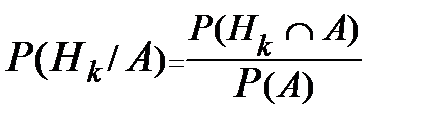 (*)
(*) = P
= P  = P (A / Hk) P (Hk)
= P (A / Hk) P (Hk)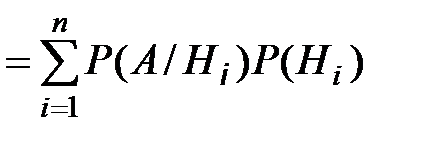

 . Из этой формулы получаем: P (H 2 / A) = 15/34. Как видно, полученная информация привела к тому, что вероятность интересующего нас события оказывается ниже априорной вероятности.
. Из этой формулы получаем: P (H 2 / A) = 15/34. Как видно, полученная информация привела к тому, что вероятность интересующего нас события оказывается ниже априорной вероятности.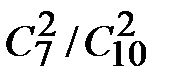 = 7/15, Р (Н 2) =
= 7/15, Р (Н 2) =  = 1/15, Р (Н 3) =
= 1/15, Р (Н 3) =  = 7/15 (при решении задачи полезно проверить выполнение необходимого условия
= 7/15 (при решении задачи полезно проверить выполнение необходимого условия  ).
). = 5/33. Если реализовалась гипотеза Н 2, то во второй урне оказалось 8 белых и 4 чёрных шара, и Р (А/Н 2) =
= 5/33. Если реализовалась гипотеза Н 2, то во второй урне оказалось 8 белых и 4 чёрных шара, и Р (А/Н 2) =  = 4/33. Легко показать, что Р (А/Н 3) =
= 4/33. Легко показать, что Р (А/Н 3) =  = 3/22. Теперь можно воспользоваться формулой полной вероятности: Р (А) = (5/33)×(7/15) + (4/33) (1/15) + (3/22) (7/15) = 47/330
= 3/22. Теперь можно воспользоваться формулой полной вероятности: Р (А) = (5/33)×(7/15) + (4/33) (1/15) + (3/22) (7/15) = 47/330 ; Р (Н 2) =
; Р (Н 2) =  ; Р (Н 3) =
; Р (Н 3) =  .
.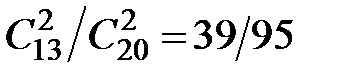 ; Р (А/Н 2) =
; Р (А/Н 2) =  ; Р (А/Н 3) =
; Р (А/Н 3) =  .
.



