Объем шара и пирамиды
Для нахождения объема шара и пирамиды построим последователь-ности вписанных в них цилиндров и призм, объемы которых известны (из очевидных соображений они равны произведению площади основания на высоту). Разрежем полушарие радиуса R равноотстоящими параллельными плоскостями на n частей и впишем в него n-1 цилиндр. Радиусы основа-ния цилиндров находятся с помощью теоремы Пифагора, объем ступенча-того тела Vn, приближающийся c ростом n к объему полушария преобразуется к виду Аналогично строится приближение пирамиды с площадью основания S и высотой h вписанными призмами с высотами h/n. Определив площади их оснований из условия подобия, получим объем ступенчатого тела Позже будет показано, что предел переменной дроби, входящей в оба приближения, равен 1/3: Используя этот результат, получим точные формулы для вычисления объемов полушария: и пирамиды: Производная функция. Геометрический смысл производной. Таблица производных. Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференцированием. Обратный процесс — интегрирование. Производной функцией Производные элементарных функций
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке
Уравнение касательной к графику функции y = f(x) в точке x0: Таблица производных основных элементарных функций 1) 2) 3) 4) 5) 6) 7) 8) 9) 19)
|



 как n-й член последовательности, сходящейся к объему пирамиды.
как n-й член последовательности, сходящейся к объему пирамиды.


 в точке x0 называется число, к которому стремится разностное отношение
в точке x0 называется число, к которому стремится разностное отношение  при Δx, стремящемся к нулю.
при Δx, стремящемся к нулю. Геометрический смысл производной
Геометрический смысл производной

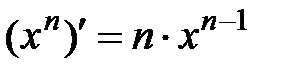 ; 10)
; 10)  ;
; ; 11)
; 11)  ;
;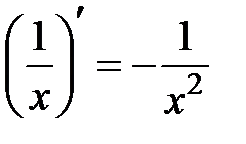 ; 12)
; 12) 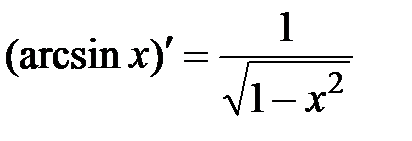 ;
; ; 13)
; 13)  ;
; ; 14)
; 14)  ;
; ; 15)
; 15)  ;
; ; 16)
; 16)  ;
; ; 17)
; 17) 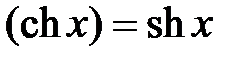 ;
; ; 18)
; 18)  ;
; .
.


