Пусть функция f(x) непрерывна на отрезке  . Если при этом f(x)
. Если при этом f(x) 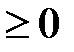 на этом отрезке, то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла:
на этом отрезке, то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла:
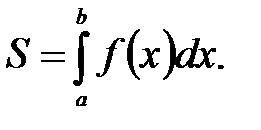
Замечания:
1. Если же

на
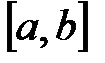
, то –
f(х) 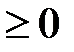
на этом отрезке. Поэтому площадь
S соответствующей криволинейной трапеции находится по формуле

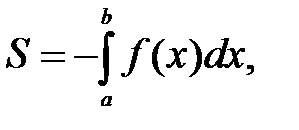
или
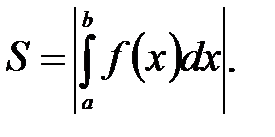
Наконец, если линия y=f(x) пересекает ось Ох, то отрезок  надо разбить на части, в пределах которых f(x) не меняет знака, и к каждой части применить ту из формул, которая ей соответствует.
надо разбить на части, в пределах которых f(x) не меняет знака, и к каждой части применить ту из формул, которая ей соответствует.
2. Площадь криволинейной фигуры, ограниченной сверху графиком функции
y2=f2(x), снизу – графиком функции
y1=f1(x), слева и справа прямыми
x=a, x=b, вычисляется по формуле:
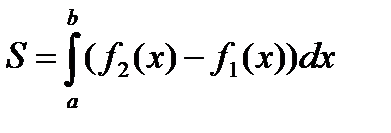
3. Площадь криволинейной фигуры, ограниченной справа графиком функции x2=j2(y), слева – графиком функции x1=j1(y), снизу и сверху прямыми y=c, y=d, вычисляется по формуле:
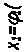

Пример 11. Найти площадь плоской фигуры, ограниченной графиком функции y = sin x и осью абсцисс при условии 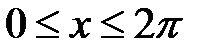 .
.
Решение: Разобьём отрезок 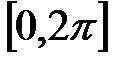 на два отрезка:
на два отрезка:  и
и 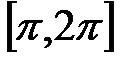 . На первом из них sin x
. На первом из них sin x 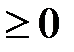 , на втором sin x
, на втором sin x 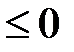 . Тогда, используя формулы, находим искомую площадь:
. Тогда, используя формулы, находим искомую площадь:
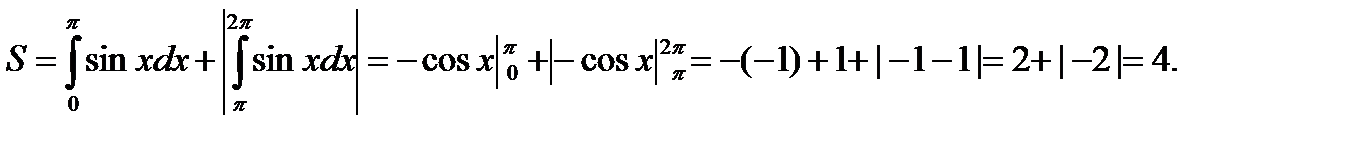
Вычисление объёмов
Если тело образовано вращением вокруг оси Ох криволинейной трапеции, ограниченной непрерывной кривой y=f(x) (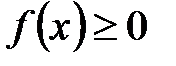 ), осью Ох и прямыми x=a, x=b (a<b), то
), осью Ох и прямыми x=a, x=b (a<b), то
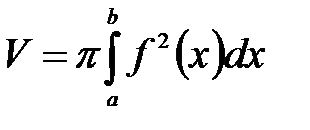
или
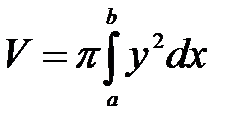
Вокруг Оу: 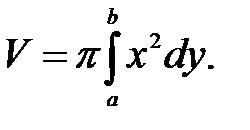
Пример 12 Найти объем тела, полученного вращением y=tgx вокруг оси Ox, 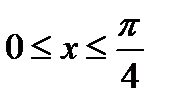 .
.
Решение:

21. Дискретные и непрерывные случайные величины. Математическое ожидание СВХ и его вычисления. Примеры с игральными костями и монетами.
 на
на 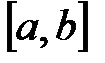 , то – f(х)
, то – f(х) 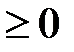 на этом отрезке. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле
на этом отрезке. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле 
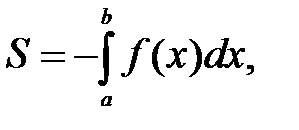
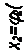
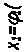
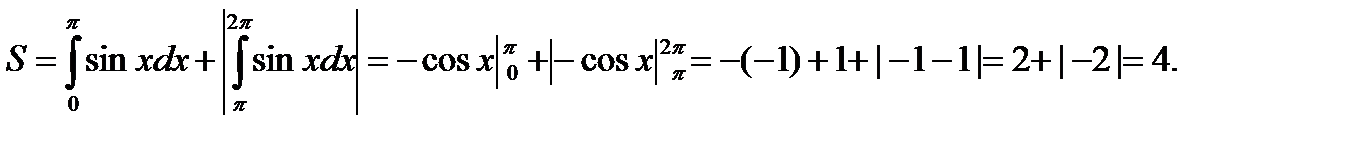
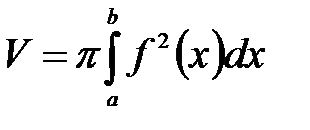 или
или 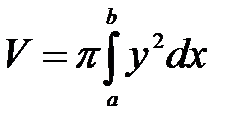

 . Если при этом f(x)
. Если при этом f(x) 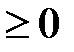 на этом отрезке, то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла:
на этом отрезке, то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла: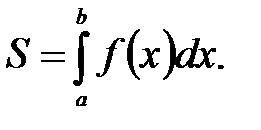
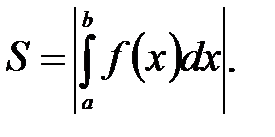
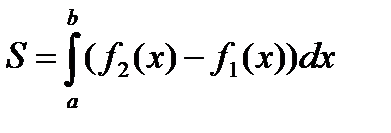

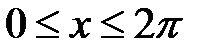 .
.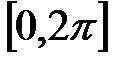 на два отрезка:
на два отрезка:  и
и 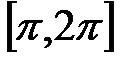 . На первом из них sin x
. На первом из них sin x 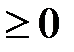 , на втором sin x
, на втором sin x 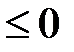 . Тогда, используя формулы, находим искомую площадь:
. Тогда, используя формулы, находим искомую площадь: 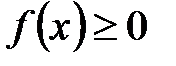 ), осью Ох и прямыми x=a, x=b (a<b), то
), осью Ох и прямыми x=a, x=b (a<b), то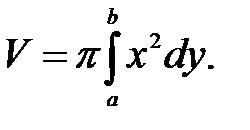
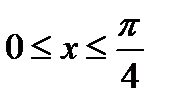 .
.




