Закон распределения дискретной случайной величины. Многоугольник распределения
Закон распределения может иметь разные формы. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. Простейшей формой задания закона распределения дискретной случайной величины X является таблица (матрица), в которой в порядке возрастания перечислены все возможные значения случайной величины и соответствующие их вероятности, т.е.
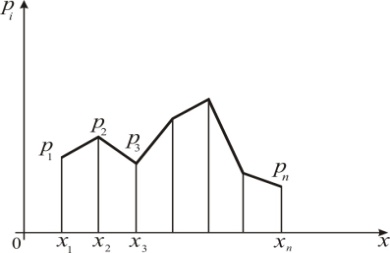
или Такая таблица называется рядом распределения дискретной случайной величины X. Графическое изображение ряда распределения (см. рис.1) называется многоугольником (или полигоном) распределения.
Рис. 1 Математическое ожидание. Дисперсия и среднее квадратическое отклонение случайной величины Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако при решении многих практических задач достаточно знать лишь некоторые числовые параметры, выражающие наиболее характерные свойства (черты) закона распределения случайной величины. Такие числа носят название числовых характеристик случайной величины. Математическим ожиданием (или средним значением) Если дискретная случайная величина X принимает конечное число значений Если же дискретная случайная величина X принимает бесконечное (счетное) число значений, то Математическое ожидание непрерывной случайной величины X с плотностью вероятности при этом математическое ожидание существует, если интеграл в правой части равенства абсолютно сходится (это значит, что сходится интеграл Дисперсией (рассеянием) Из определения вытекает часто используемая формула: Если Если X-непрерывная случайная величина с плотностью Средним квадратическим отклонением случайной величины Среднее квадратическое отклонение есть мера рассеяния значений случайной величины около ее математического ожидания.
|

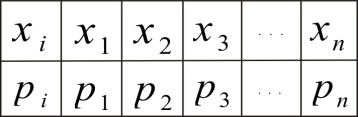
 , где
, где 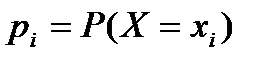 ;
; 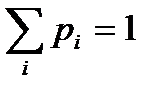 .
.
 (или
(или  ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.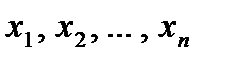 , то ее математическое ожидание
, то ее математическое ожидание 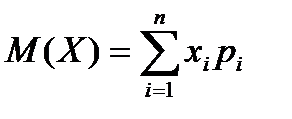 (3)
(3) , (4) при этом математическое ожидание существует, если ряд в правой части этой формулы абсолютно сходится, т. е. сходится ряд
, (4) при этом математическое ожидание существует, если ряд в правой части этой формулы абсолютно сходится, т. е. сходится ряд 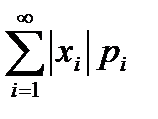 .
. ,находится по формуле
,находится по формуле  , (5)
, (5) ).
). (или
(или 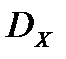 ) случайной величины
) случайной величины  называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:  .
. .
. , (т. е.
, (т. е. 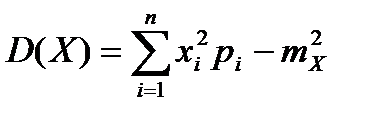 ) (6)в случае конечного числа значений, принимаемых случайной величиной X, и по формуле
) (6)в случае конечного числа значений, принимаемых случайной величиной X, и по формуле 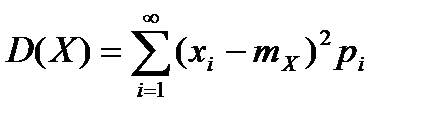 , (т. е.
, (т. е.  ) (7) в случае счетного числа значений.
) (7) в случае счетного числа значений.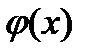 , то
, то  (или
(или  ). (8)
). (8) называется величина
называется величина 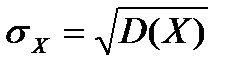 .
.


