Формула Бернулли вычисления вероятности. Математическое ожидание и дисперсия в этом случае. Примеры.
Формула Бернулли. Производятся n независимых испытаний, в каждом из которых может произойти некоторое событие А (по традиции такой исход опыта называется успехом) с одной и той же вероятностью в частности, следует, что вероятность того, что в n испытаниях, удовлетворяющих схеме Бернулли, событие А наступит: 1)менее 2)более 3) хотя бы один раз — равна 4) не менее Число Если в каждом независимом испытании вероятность наступления события А равна функция называется производящей функцией Пример1. Игральную кость подбрасывают 10 раз. Найти вероятность того, что шестерка выпадет: a) ровно 2 раза; b) не более 8 раз; c) хотя бы один раз Решение: Проводится 10 независимых испытаний. Каждое испытание имеет два исхода: выпадет шестерка, не выпадет шестерка. Вероятность выпадения шестерки в каждом испытании постоянна и равна a) Здесь
Однако в этом случае удобно найти вероятность противоположного события – «шестерка выпадет более 8 раз» т.е. 9 или 10
b) Искомая вероятность равна Пример 2. Всхожесть семян данного сорта растений составляет 70%. Найти наивероятнейшее число всхожих семян в партии из 240 семян. Решение:Наивероятнейшее число находим из двойного неравенства Поскольку
Отсюда следует, что Ответ: 168 Пример 3. Прибор состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента за время Решение:Так как
Отсюда следует, что
|
или произойти противоположное событие А (такой исход называют неудачей) с вероятностью 
. Тогда вероятность того, что событие А наступит ровно m раз, находится по формуле Бернулли 
раз — равна 
раз и не более 
раза — равна: 
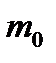называется наивероятнейшим числом наступлений (или наиболее вероятным числом успехов) в схеме Бернулли, если вероятности p и q отличны от нуля то число 
(
числа разные), то вероятность 
того, что в этой серии испытаний событие А наступит m раз, равна коэффициенту при m – ой степени многочлена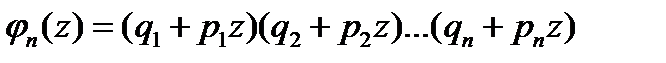 
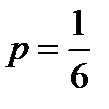. Таким образом, мы имеем дело со схемой испытаний Бернулли. Для нахождения искомых вероятностей используем схему Бернулли.
Отсюда, 
b) Искомая вероятность равна:
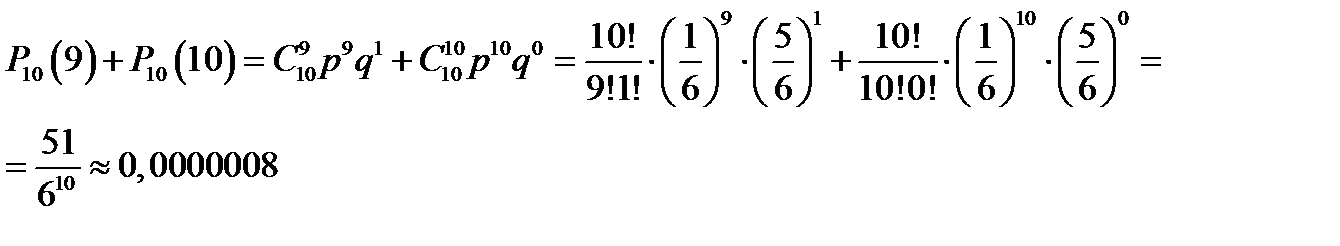Итак, вероятность того, что шестерка выпадет не более 8 раз, равна 
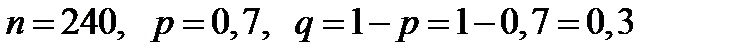, то
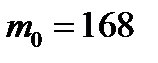
равны 
. Найти вероятность того, что откажут два элемента.
. Составим производящую функцию:
