Формула Бернулли
Часто встречаются задачи, в которых одно и то же испытание повторяется многократно. В результате каждого испытания может появиться или не появиться некоторое событие Определение 1. Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода – появление события Теорема (формула Бернулли). Вероятность того, что в Доказательство. Все 1) Число благоприятных исходов равно числу способов, которыми можно расположить 2) Вероятность каждого отдельного исхода можно подсчитать по формуле произведения вероятностей независимых событий. Например, вероятность появления комбинации: Поскольку все исходы являются несовместными событиями, то вероятность, что событие Определение 2. Числа Пример 1. Для контроля качества из партии деталей отбирается 5 деталей. Партия бракуется, если в выборке хотя бы две бракованные детали. Найти вероятность того, что партия будет забракована, если каждая деталь может оказаться бракованной с вероятностью 0,01. Решение. Найдем вероятность того, что в выборке из 5 деталей будет не более одной бракованной детали:
Тогда вероятность того, что партия будет забракована: Если каждое испытание имеет
Доказательство формулы аналогично случаю двух исходов.
|

 . Нас будет интересовать число наступлений события
. Нас будет интересовать число наступлений события  в серии из
в серии из  испытаний.
испытаний.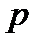 , а неудача с вероятностью
, а неудача с вероятностью  .
. испытаниях по схеме Бернулли “успех” наступит ровно
испытаниях по схеме Бернулли “успех” наступит ровно  раз:
раз:  (1.19)
(1.19) испытаний можно рассматривать как одно сложное испытание, имеющее
испытаний можно рассматривать как одно сложное испытание, имеющее  возможных исходов. (Например, при
возможных исходов. (Например, при  возможные исходы такого сложного испытания –
возможные исходы такого сложного испытания –  ).
). успехов на
успехов на  .
.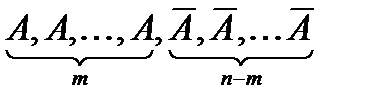 равна
равна  . Очевидно, что вероятности остальных комбинаций равны также
. Очевидно, что вероятности остальных комбинаций равны также  .
. раз:
раз:  .
.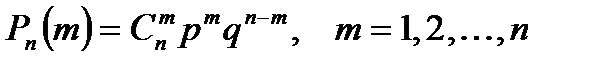 называются биномиальными вероятностями.
называются биномиальными вероятностями. .
. .
.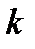 исходов, вероятности которых
исходов, вероятности которых  ,
,  , то вероятность того, что в
, то вероятность того, что в  испытаниях первый исход появится
испытаниях первый исход появится  раз, второй исход появится
раз, второй исход появится 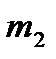 раз и т.д. определится по формуле:
раз и т.д. определится по формуле: . (1.20)
. (1.20)


