В наиболее общем виде этот закон называют предельным в силу того, что к нему приближаются другие законы распределения непрерывных случайных величин и даже сочетания этих законов при определенных часто встречающихся на практике условиях. При нормальном распределении случайная величина может принимать любые значения в интервале от  до
до  . Распределение случайной величины всегда подчиняется нормальному закону, если она зависит от большого числа однородных по своему воздействию факторов. Причем влияние каждого из них по сравнению со всей их совокупностью незначительно. В общем случае выражение для плотности распределения имеет вид
. Распределение случайной величины всегда подчиняется нормальному закону, если она зависит от большого числа однородных по своему воздействию факторов. Причем влияние каждого из них по сравнению со всей их совокупностью незначительно. В общем случае выражение для плотности распределения имеет вид
 , (3.4)
, (3.4)
где  - среднее квадратическое отклонение наработки до отказа,
- среднее квадратическое отклонение наработки до отказа,  - математическое ожидание наработки до отказа (средняя наработка до отказа).
- математическое ожидание наработки до отказа (средняя наработка до отказа).
Кривая нормального распределения имеет колоколообразный вид симметричный относительно центра рассеяния в точке  . Если изменять положение центра рассеяния, т.е. изменять величину
. Если изменять положение центра рассеяния, т.е. изменять величину  , не изменяя среднего квадратичного отклонения, то кривая будет смещаться вдоль оси времени без изменения своей формы (рис. 3.1).
, не изменяя среднего квадратичного отклонения, то кривая будет смещаться вдоль оси времени без изменения своей формы (рис. 3.1).
Расчеты показывают, что вероятность нахождения значения нормально распределенной величины в интервале 1 длиной

, расположенной вправо от центра рассеяния, равна 34%, а в интервалах 2 и 3 той же длины, соответственно 14% и 2%. Аналогичные значения вероятности получаются и в случае расположения интервалов длиной
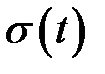
влево от центра рассеяния в силу симметричности кривой распределения. Другими словами 50% возможных отклонений находятся вправо от центра рассеяния на длине
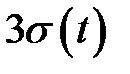
и 50% значений отклонения укладываются на участке

с левой стороны. Из сказанного выше следует, что при нормальном распределении весь разброс значений случайной величины практически заключен в интервале времени

.
Параметр

характеризует форму кривой распределения. Из выражения (3.4) видно, что наибольшая ордината кривой распределения, равная

, обратно пропорциональна

. Поскольку площадь под кривой всегда равна единице, то при различных значениях

происходит трансформация кривой распределения согласно рис. 3.2.
Вероятность безотказной работы при нормальном распределении записывается выражением
 . (3.5)
. (3.5)
Рассмотренное распределение чаще всего используется для описания отказов. Вызванных постепенным изменением параметров приборов, а также при оценке надежности элементов на стадии старения. Кроме того, нормальному закону, как правило, подчиняются распределения электрических параметров полупроводниковых приборов и ИМС.
 , расположенной вправо от центра рассеяния, равна 34%, а в интервалах 2 и 3 той же длины, соответственно 14% и 2%. Аналогичные значения вероятности получаются и в случае расположения интервалов длиной
, расположенной вправо от центра рассеяния, равна 34%, а в интервалах 2 и 3 той же длины, соответственно 14% и 2%. Аналогичные значения вероятности получаются и в случае расположения интервалов длиной 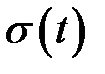 влево от центра рассеяния в силу симметричности кривой распределения. Другими словами 50% возможных отклонений находятся вправо от центра рассеяния на длине
влево от центра рассеяния в силу симметричности кривой распределения. Другими словами 50% возможных отклонений находятся вправо от центра рассеяния на длине 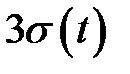 и 50% значений отклонения укладываются на участке
и 50% значений отклонения укладываются на участке  с левой стороны. Из сказанного выше следует, что при нормальном распределении весь разброс значений случайной величины практически заключен в интервале времени
с левой стороны. Из сказанного выше следует, что при нормальном распределении весь разброс значений случайной величины практически заключен в интервале времени  .
.
 характеризует форму кривой распределения. Из выражения (3.4) видно, что наибольшая ордината кривой распределения, равная
характеризует форму кривой распределения. Из выражения (3.4) видно, что наибольшая ордината кривой распределения, равная  , обратно пропорциональна
, обратно пропорциональна  . Поскольку площадь под кривой всегда равна единице, то при различных значениях
. Поскольку площадь под кривой всегда равна единице, то при различных значениях  происходит трансформация кривой распределения согласно рис. 3.2.
происходит трансформация кривой распределения согласно рис. 3.2.

 до
до  . Распределение случайной величины всегда подчиняется нормальному закону, если она зависит от большого числа однородных по своему воздействию факторов. Причем влияние каждого из них по сравнению со всей их совокупностью незначительно. В общем случае выражение для плотности распределения имеет вид
. Распределение случайной величины всегда подчиняется нормальному закону, если она зависит от большого числа однородных по своему воздействию факторов. Причем влияние каждого из них по сравнению со всей их совокупностью незначительно. В общем случае выражение для плотности распределения имеет вид , (3.4)
, (3.4) - математическое ожидание наработки до отказа (средняя наработка до отказа).
- математическое ожидание наработки до отказа (средняя наработка до отказа). . Если изменять положение центра рассеяния, т.е. изменять величину
. Если изменять положение центра рассеяния, т.е. изменять величину 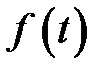
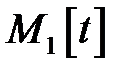



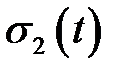


 . (3.5)
. (3.5)


