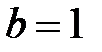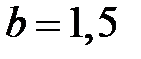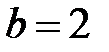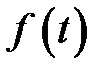В ряде случаев для представления распределения показателей надежности приборов на начальном этапе эксплуатации используют логарифмически нормальное распределение, при котором логарифм случайной величины подчиняется нормальному закону распределения. В этом случае выражение для плотности вероятности имеет вид
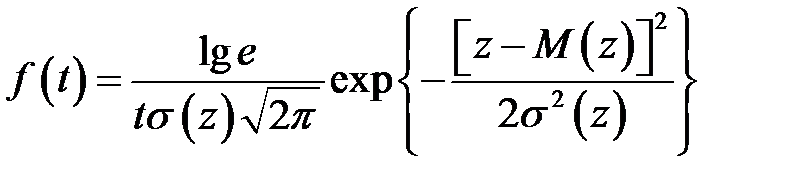 , (3.6)
, (3.6)
где 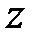 - десятичный логарифм исследуемой случайной величины (в данном случае логарифм случайной наработки до отказа),
- десятичный логарифм исследуемой случайной величины (в данном случае логарифм случайной наработки до отказа), 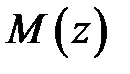 - математическое ожидание логарифма наработки до отказа,
- математическое ожидание логарифма наработки до отказа, 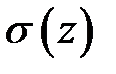 - среднее квадратическое отклонение величины
- среднее квадратическое отклонение величины 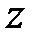 .
.
Среднее время безотказной работы при логарифмически нормальном распределении рассчитывается по формуле
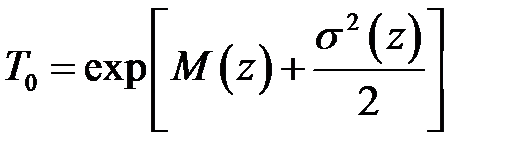 . (3.7)
. (3.7)
Распределение Вейбулла – Гнеденко.
Для описания показателей надежности полупроводниковых приборов и ИМС на начальном этапе эксплуатации часто используется распределение Вейбулла – Гнеденко, характеризуемое двумя параметрами: параметром масштаба 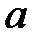 и параметром формы
и параметром формы 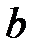 . Показатели надежности определяются следующими выражениями:
. Показатели надежности определяются следующими выражениями:
вероятность безотказной работы
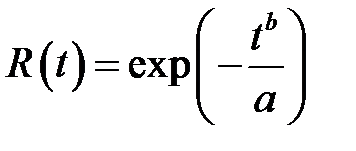 , (3.8)
, (3.8)
плотность вероятности отказов
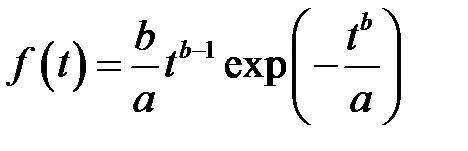 , (3.9)
, (3.9)
интенсивность отказов
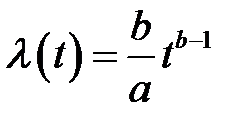 . (3.10)
. (3.10)
Особенностью этого распределения является то, что с изменением параметра формы 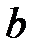 , изменяется, и характер зависимости показателей надежности от времени. Так, например, для
, изменяется, и характер зависимости показателей надежности от времени. Так, например, для 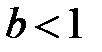 интенсивность отказов будет монотонно убывающей функцией, а при
интенсивность отказов будет монотонно убывающей функцией, а при 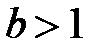 - монотонно возрастающей. Данное свойство распределения позволяет соответствующим подбором параметров
- монотонно возрастающей. Данное свойство распределения позволяет соответствующим подбором параметров 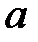 и
и 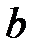 обеспечить хорошее совпадение результатов опытных данных с аналитическими выражениями показателей распределения. Так при постоянной величине
обеспечить хорошее совпадение результатов опытных данных с аналитическими выражениями показателей распределения. Так при постоянной величине 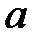 кривые распределения плотности вероятности от времени при различных значениях
кривые распределения плотности вероятности от времени при различных значениях 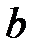 будут иметь вид показанный на рис. 3.3. Большинство полупроводниковых приборов и ИМС на начальном периоде времени эксплуатации имеет распределение наработки до отказа, подчиняющееся закону Вейбулла – Гнеденко, с показателем формы
будут иметь вид показанный на рис. 3.3. Большинство полупроводниковых приборов и ИМС на начальном периоде времени эксплуатации имеет распределение наработки до отказа, подчиняющееся закону Вейбулла – Гнеденко, с показателем формы 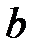 меньше или близким к единице.
меньше или близким к единице.

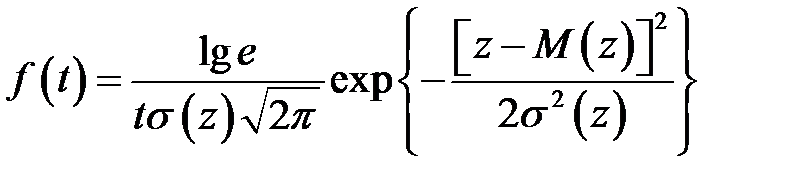 , (3.6)
, (3.6)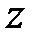 - десятичный логарифм исследуемой случайной величины (в данном случае логарифм случайной наработки до отказа),
- десятичный логарифм исследуемой случайной величины (в данном случае логарифм случайной наработки до отказа), 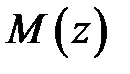 - математическое ожидание логарифма наработки до отказа,
- математическое ожидание логарифма наработки до отказа, 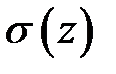 - среднее квадратическое отклонение величины
- среднее квадратическое отклонение величины 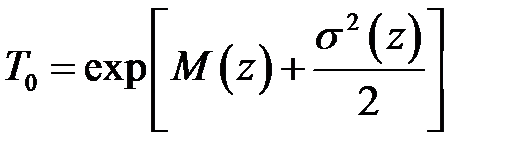 . (3.7)
. (3.7)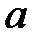 и параметром формы
и параметром формы 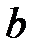 . Показатели надежности определяются следующими выражениями:
. Показатели надежности определяются следующими выражениями: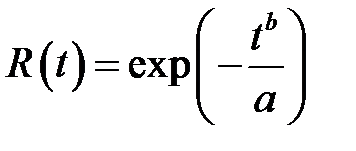 , (3.8)
, (3.8)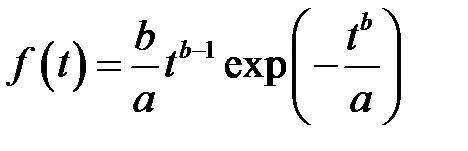 , (3.9)
, (3.9)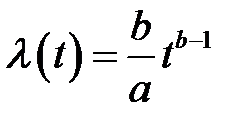 . (3.10)
. (3.10)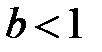 интенсивность отказов будет монотонно убывающей функцией, а при
интенсивность отказов будет монотонно убывающей функцией, а при 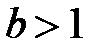 - монотонно возрастающей. Данное свойство распределения позволяет соответствующим подбором параметров
- монотонно возрастающей. Данное свойство распределения позволяет соответствующим подбором параметров 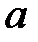 и
и