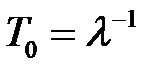Экспоненциальный закон.
Наибольшую популярность и широкое применение в теории и практике надежности нашло так называемое экспоненциальное распределение. Его специфической особенностью является постоянство интенсивности отказов во времени. Для данного распределения вероятность безотказной работы задается выражением
Последнее выражение можно получить из формулы (2.12), если в ней положить взяв два первых члена разложения:
Воспользовавшись равенством (3.12), получим для вероятности наступления отказа
плотности вероятности отказа
средней наработке до отказа
Графически все эти функции показаны на рис. 3.4. В качестве примера, для экспоненциального закона распределения при Таблица 3.1.
32. Распределение Пуассона случайной величины. Примеры. 33. Нормальное распределения СВХ. Вероятность попадания СВХ в заданный промежуток для этого случая.
* Если точные значения границ интервала неизвестны, то рассматривают интервал (-¥, + ¥).
|
. (3.11.)
. В случаях, когда 
, можно использовать упрощенное выражение для 
, разложив (3.11) в степенной ряд и
. (3.12)
; (3.13)
; (3.14)
. (3.15)
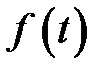
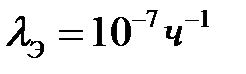и количестве элементов 
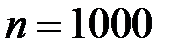в изделии получим следующие результаты расчета показателей надежности, которые приведены в табл. 3.1.
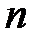в аппаратуре, шт.
, 
.
, 
.
, 
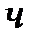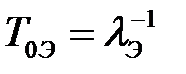
