Решение. Возможные значения С В X - число сданных экзаменов - 0, I, 2.Возможные значения С В X - число сданных экзаменов - 0, I, 2. Пусть событие Считая что курсант не сдаст экзамены
что сдаст один экзамен
что сдаст два экзамена
Ряд распределения и многоугольник распределения будут иметь вид
Закон распределения ССВ может быть задан в различных формах. Одной из форм задания является таблица распределения СДСВ. Пусть X и У - ДСВ, возможные значения которых
Такая таблица называется таблицей (матрицей) распределения СДСВ с конечным числом возможных значений. Все возможные события
Итоговые столбец или строка таблицы распределения представляют соответственно распределение одномерных составляющих
Действительно, распределение одномерной СВХ можно получить, вычислив вероятность события
Аналогично
Таким образом, чтобы по таблице распределения найти вероятность того, что одномерная СВ приняла определенное значение, надо просуммировать вероятности Если зафиксировать значение одного аргумента, например, положить Вероятности Из определения условной вероятности Аналогично условнее распределение СВУ при условии
31. Распределения СВХ определяемое формулой Бернулли. Пример. Основные законы распределения случайных величин
Рассмотренные выше соотношения справедливы для любых типов невосстанавливаемых изделий, законы распределения показателей надежности которых, заранее известны. Однако применимость их для расчета показателей надежности полупроводниковых приборов и ИМС а так же для прогнозирования деградации последних на длительный период ограничена. Это связано с тем, что полупроводниковые приборы и микросхемы имеют сравнительно высокую надежность и их отказы являются весьма редким событием. Поэтому для получения достаточно достоверной информации при проведении расчетов показателей надежности, необходимо проводить длительные испытания (в течение десятков и сотен тысяч часов). Кроме того, отсутствие данных о законах распределения отказов не позволяют распространять результаты расчетов показателей надежности за пределы временных испытаний и прогнозировать надежность приборов на длительный период. Указанные обстоятельства вызывают необходимость полученные в результате испытаний распределения наработки до отказа аппроксимировать эмпирически математическими выражениями, либо использовать для описания экспериментальных данных известные законы распределения случайных величин, под которыми понимаются соответствие между возможными значениями случайных величин и их вероятностями. Биноминальный закон. Биноминальный закон распределения характеризует вероятность появления события А n раз в m независимых испытаниях. Если вероятность появления события А в одном опыте равна r (соответственно вероятность его не появления равна где Биноминальным закон распределения назван потому, что правую часть равенства (3.1) можно рассматривать как общий член разложения бинома Ньютона. Биноминальный закон распределения применяется при статическом контроле при ограниченной информации о свойствах приборов, которые необходимо расклассифицировать на годные и дефектные.
|
состоит в том, что курсант сдает i -й экзамен (i =1, 2).
и 
независимыми, будем иметь вероятность того,
,
,
.
, где 
, 
. Тогда распределение системы таких СВ может быть охарактеризовано указанием вероятностей 
того, что СВ X примет значение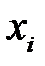 
и одновременно с этим С В У примет значение 
. Вероятности 
сводятся в таблицу вида
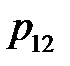
составляют полную группу несовместных событий, поэтому
или 
.
, как сумму вероятностей несовместных событий
из соответствующей этому значению строки (столбца) данной таблицы.
, то полученное распределение СВХ называется условным распределением X при условии 
.
этого распределения будут условными вероятностями события 
, найденными при условии, что событие 
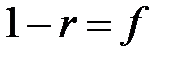), а число независимых испытаний равно m, то вероятность появления события А n раз в серии m испытаний 
может быть представлена математической формулой биноминального закона распределения следующим образом 
, (3.1)
- число сочетаний m по n, равное 
.
