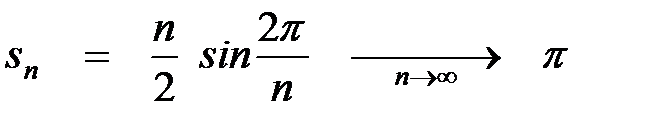Доказательство.
Пусть Произведение
5. Частное двух сходящихся последовательностей На основании перечисленных свойств можно находить пределы числовых последовательностей. Рассмотрим некоторые примеры. 3. Найти предел Отношение двух сходящихся есть последовательность сходящаяся и поэтому 4. 1.3. Число «е» Числом «е» называется предел последовательности с общим членом Применив формулу бинома Ньютона, найдем Учитывая неравенство где Получили, что Это число определил Леонард Эйлер (1707 – 1783) – великий математик, член Петербургской Академии наук, большую часть жизни проведший в России, по происхождению швейцарец. При помощи современных ЭВМ, это число вычислено с точностью до 590 знаков после запятой. Отдавая дань Эйлеру, это число называют числом «е »: е =2,718281… Число е играет огромную роль в математике. Рассмотрим примеры. 1. 2. 3.
П редел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого 1.1. Применения пределов 1.2.1. Площадь круга
Для вычисления площади круга единичного радиуса опишем вокруг него правильный n-угольник. Его площадь, равная n площадям одинако-вых равнобедренных треугольников с вершинами в т. О, даст приближение площади круга с избытком. Площадь одного треугольника равна произве-дению единичной высоты на половину основания, равную тангенсу угла Например, площадь правильного треугольника: площадь описанного квадрата: площадь описанного шестиугольника: Монотонно убывающая последовательность Sn сходится к числу Последовательность площадей правильных многоугольников, вписанных в окружность, дает приближения площади круга с недостатком. Площадь одного из n равнобедренных треугольников, составляющих вписанный n-угольник, можно вычислить, как половину произведения единичных сторон на синус угла
|

 ,
,  ,тогда
,тогда  ,
,  , где
, где  и
и  – бесконечно малые последовательности.
– бесконечно малые последовательности. , а
, а  .
. является суммой бесконечно малых последовательностей и сама является бесконечно малой, например,
является суммой бесконечно малых последовательностей и сама является бесконечно малой, например,  . Тогда
. Тогда  и следовательно
и следовательно  .
. и
и  при условии, что предел
при условии, что предел  отличен от нуля, есть последовательность сходящаяся, а её предел равен частному пределов (без доказательства).
отличен от нуля, есть последовательность сходящаяся, а её предел равен частному пределов (без доказательства). . При делении числителя и знаменателя дроби на одно и то же число, дробь не меняется. Разделим числитель и знаменатель на n2 и получим
. При делении числителя и знаменателя дроби на одно и то же число, дробь не меняется. Разделим числитель и знаменатель на n2 и получим 

 т.к.
т.к. 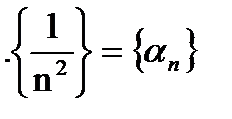 ,
,  т.к.
т.к. 
 .
.
 .
.
 , для любого
, для любого  , получим
, получим  и
и  ,
, – сумма бесконечно убывающей геометрической прогрессии
– сумма бесконечно убывающей геометрической прогрессии  ,
, 
 , т.е. предел последовательности – это некоторое число, лежащее на интервале (2;3).
, т.е. предел последовательности – это некоторое число, лежащее на интервале (2;3).
 .
. .
.

 > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала (a -
> 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала (a -  ; площадь Sn всего n-угольника будет в n раз больше:
; площадь Sn всего n-угольника будет в n раз больше:  .
. ;
;

 - площади круга единичного радиуса.
- площади круга единичного радиуса. между ними; обозначив через sn площадь всего n-угольника, получим монотонно возрастающую последовательность приближений, стремящихся к площади круга снизу:
между ними; обозначив через sn площадь всего n-угольника, получим монотонно возрастающую последовательность приближений, стремящихся к площади круга снизу: