Числовая последовательность и ее придел. Применение понятия придела к вычислению площади круга.
Числовые последовательности Определение 1.1.1. Если каждому n из множества натурального ряда чисел поставлено в соответствие по определённому закону некоторое вещественное число x n, то множество чисел x 1, x 2, x 3,…., x n,…. называется числовой последовательностью и обозначается { x n}, при этом x n называется общим членом числовой последовательности. Числа x n называются элементами или членами числовой последовательности. Например, последовательность с общим членом x n= Последовательность с общим членом x n=1+(-1)n будет последовательностью чисел Арифметическая и геометрическая прогрессия также являются числовыми последовательностями. Арифметическая прогрессия – это числовая последовательность с общим членом x n= x 1+ Например, 1, 5, 9, …, 4n-3, …; x n=1+4(n-1)=4n-3, d =4 Геометрическая прогрессия – это числовая последовательность с общим членом Например: 3, Бесконечно большие и бесконечно малые последовательности Числовые последовательности бывают бесконечно большими и бесконечно малыми. Определение 1.1.2. Последовательность { xn } называется бесконечно большой, если для любого положительного числа А, сколь угодно большого, можно указать номер N такой, что при n Например, последовательность натурального ряда чисел 1, 2, …, n, … является бесконечно большой, т.к, какое ни возьми число N, начиная с которого, для n Последовательность 1, 2, 1, 3, 1, 4, …, 1, n, … не является бесконечно большой, так как для всех нечетных членов этой последовательности неравенство Определение 1.1.3. Последовательность { Например, геометрическая прогрессия, у которой знаменатель Рассмотрим геометрическую прогрессию с общим членом Изобразим точками на числовой оси элементы этой последовательности (см.рис.1.1.)
Выберем сколь угодно малое число Если в неравенстве Рассмотрим пример последовательности с общим членом xn=(-1) 1, Изобразим точками на числовой оси элементы этой последовательности (см. рис.1.2)
Рис.1.2. Числовая последовательность с общим членом xn=(-1) Видно, что члены последовательности приближаются к нулю, при этом ни один элемент последовательности не равен нулю. Для любого, сколь угодно малого,
Значит, последовательность также является бесконечно малой. Основные свойства бесконечно малых последовательностей 1. Сумма бесконечно малых последовательностей есть последовательность бесконечно малая. 2. Разность двух бесконечно малых последовательностей есть последовательность бесконечно малая 3. Произведение любого конечного числа бесконечно малых последовательностей есть последовательность бесконечно малая 4. Если { xn} – бесконечно большая последовательность, то, начиная с некоторого номера n, определена последовательность 5. Если все члены бесконечно малой последовательности Сходящиеся последовательности. Свойства сходящихся последовательностей Определение 1.2.1. Последовательность { xn } называется сходящейся, если существует такое число а, что последовательность Определение 1.2.2. Последовательность { xn} называется сходящейся, если существует такое число а, что для любого сколь угодно малого положительного Очевидно, что оба определения дополняют друг друга. Действительно, из «Определения 1.2.1» утверждение Неравенство Будем говорить, что xn попадает в Так как Рассмотрим примеры сходящихся последовательностей. 1. Последовательность
Составим последовательность Докажем, что последовательность 2. Последовательность Действительно, Свойства сходящихся последовательностей 1. Сходящаяся последовательность имеет только один предел (без доказательства). 2. Сумма сходящихся последовательностей Доказательство. Пусть Сумма 3. Разность сходящихся последовательностей 4. Произведение сходящихся последовательностей есть последовательность сходящаяся, а её предел равен произведению пределов.
|

 , будет последовательностью чисел 1,
, будет последовательностью чисел 1,  ,
,  ,…..,=
,…..,=  .
.
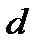 (n-1), где d – разность арифметической прогрессии
(n-1), где d – разность арифметической прогрессии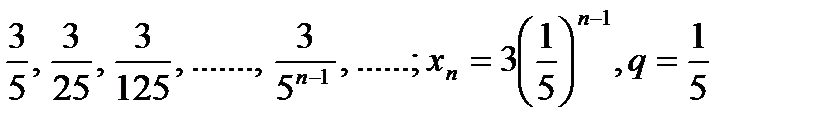 .
. N все элементы последовательности xn удовлетворяют неравенству
N все элементы последовательности xn удовлетворяют неравенству 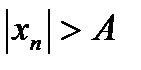
 n } называется бесконечно малой, если для любого положительного числа
n } называется бесконечно малой, если для любого положительного числа 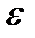 , сколь угодно малого, можно указать номер N такой, что при n
, сколь угодно малого, можно указать номер N такой, что при n  .
. , является бесконечно малой числовой последовательностью.
, является бесконечно малой числовой последовательностью. 1,
1, 
 Рис.1.1. Числовая последовательность с общим членом
Рис.1.1. Числовая последовательность с общим членом 
 <
< 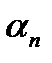 <
<  ,
,

 .
. .
. .
. , которая является бесконечно малой.
, которая является бесконечно малой. 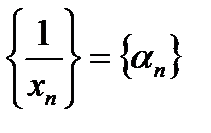 .
. не равно нулю, то последовательность
не равно нулю, то последовательность  бесконечно большая.
бесконечно большая.  .
.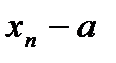 является бесконечно малой. При этом число а называется пределом последовательности { xn } и обозначается
является бесконечно малой. При этом число а называется пределом последовательности { xn } и обозначается  , или
, или  при
при 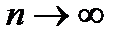 .
. все элементы последовательности xn удовлетворяют неравенству
все элементы последовательности xn удовлетворяют неравенству 
 - бесконечно малая, следует, что
- бесконечно малая, следует, что  для любого
для любого 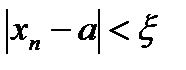 эквивалентно неравенству
эквивалентно неравенству 
 , то общий член
, то общий член  , или
, или 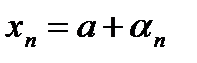 . Будем говорить, что любой элемент сходящейся последовательности может быть записан в виде
. Будем говорить, что любой элемент сходящейся последовательности может быть записан в виде  , где
, где  - элемент бесконечно малой последовательности.
- элемент бесконечно малой последовательности. сходится.
сходится.

 бесконечно малая. Если
бесконечно малая. Если  , и поэтому по данному
, и поэтому по данному  или
или 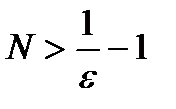 .
. сходится к числу а =2.
сходится к числу а =2.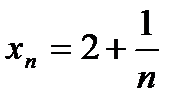 , тогда последовательность
, тогда последовательность  бесконечно малая.
бесконечно малая. и
и  есть последовательность сходящаяся, а её предел равен сумме пределов.
есть последовательность сходящаяся, а её предел равен сумме пределов. ,
,  – бесконечно малая последовательность,
– бесконечно малая последовательность,  , тогда
, тогда  ,
,  – бесконечно малая последовательность.
– бесконечно малая последовательность. . Общий член последовательности может быть записан
. Общий член последовательности может быть записан 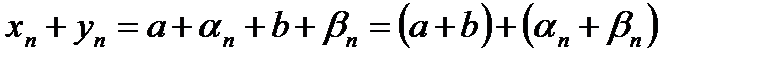 , т.к.
, т.к.  есть сумма двух бесконечно малых последовательностей и является бесконечно малой последовательностью, то
есть сумма двух бесконечно малых последовательностей и является бесконечно малой последовательностью, то 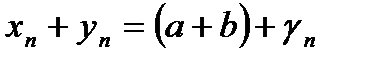 , где
, где  , то
, то  .
.


