Геометрическая вероятность(линейный плоский объемный случаи). Примеры.

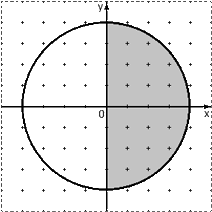
Геометрическая вероятность

Классическое определение вероятности связано с понятием элементарного события. Рассматривается некий набор Ω равновероятных событий Ai, которые в совокупности дают достоверное событие. И тогда все хорошо: всякое событие разбивается на элементарные, после чего считается его вероятность.

Однако, далеко не всегда исходный набор Ω (т.е. пространство всех элементарных событий) является конечным. Например, в качестве Ω можно взять ограниченное множество точек на плоскости или отрезок на прямой.

В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.

Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.

Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме по-любому больше P(Ω) = 1.

Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.

Определение

Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω:

Задача

Мишень имеет форму окружности радиуса 4. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены.

Решение

Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем:

Ответ

0,5

Чтобы наглядно представить себе, что такое геометрическая вероятность, возьмите лист бумаги и начертите произвольную фигуру. Треугольник, квадрат или окружность — что угодно. Затем возьмите острый, хорошо заточенный карандаш и ткните им в любую точку фигуры. Повторите этот нехитрый процесс несколько раз. Если исключить попадания за пределами фигуры, то получится вот что:

Вероятность попадания в фигуру равна P(Ω) = 1. Это вполне логично, поскольку вся наша фигура — это и есть пространство элементарных событий Ω;

Если некоторую точку (элементарное событие) отметить заранее, то вероятность попадания именно в нее равна нулю. Даже если специально «целиться», точного попадания не будет. Ошибка составит тысячные доли миллиметра, но не ноль;

Теперь возьмем две точки. Вероятность попадания в любую из них все равно ноль. Аналогично, если взять 3 точки. Или пять — без разницы.

Этот опыт показывает, что конечная сумма нулевых слагаемых всегда равна нулю. Но что происходит, когда слагаемых становится бесконечно много? Здесь ситуация не так однозначна, и возможны три варианта:

Сумма равна нулю, как и для конечного набора точек. Если в нашем опыте отмечать точки до бесконечности, вероятность попадания в их объединение все равно нулевая;

Сумма равна некоторому положительному числу — этот случай принципиально отличается от первого. Здесь и возникает геометрическая вероятность;

Сумма равна бесконечности — бывает и такое, но сейчас нас это не интересует.

Почему так происходит? Механизм возникновения положительных чисел и бесконечностей связан с понятием счетности множества. Кроме того, надо понимать, что такое мера Лебега. Впрочем, эти знания действительно нужны вам, только если вы учитесь на математика.