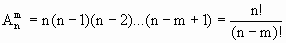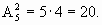Перестановки элемента множества. Число постановок Рn . Примеры.
В комбинаторике перестано́вка — это упорядоченный набор чисел В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.) Число всех перестановок порядка равно числу размещений из n по n, то есть факториалу: Композиция определяет операцию произведения на перестановках одного порядка: Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий. Основная формула комбинаторики Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*...*nk. Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n1 элементов, а вторая - из n2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n2. Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n2. Так как в первой группе всего n1 элемент, всего возможных вариантов будет n1*n2. Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться? Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6). Итак, N=n1*n2*n3=6*7*4=168. В том случае, когда все группы состоят из одинакового числа элементов, т.е. n1=n2=...nk=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно nk.Такой способ выбора носит название выборки с возвращением. Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8? Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=54=625. Рассмотрим множество, состоящие из n элементов. Это множество будем называть генеральной совокупностью. Определение 1. Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов. Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком. Число размещений обозначается Anm и вычисляется по формуле: Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1. Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные? Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет: Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов. Пример 6. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}. Число сочетаний обозначается Cnm и вычисляется по формуле: Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся? Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно: Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов. Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2). Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд? Решение: эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг. Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно. Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов). Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны. И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере. Пример. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек? Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5. Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5. Число перестановок - число различных способов, которыми может быть упорядочено данное множество, состоящее из n элементов. Нахождение числа перестановок из n элементов. Pn (P – первая буква французского слова permutation – перестановка). Читается: “Число перестановок из эн элементов” или “Пэ из эн”. В задании 1 было показано P4 = 4*3*2*1 = 1*2*3*4 (по переместительному свойству умножения). Pn=1*2*3*…*n (1) т.о., число перестановок из n элементов равно произведению всех натуральных чисел от 1 до n. При использовании символа n! формула (1) принимает вид Pn= n! (Учащимся: правило нахождения перестановок из n элементов записать в тетрадь словами и формулой, выучить, рассказать соседу по парте). Пример 1. В расписании 7 класса на четверг должно быть 6 предметов: русский язык, литература, алгебра, география, физика, физкультура. Сколькими способами можно составить расписание на этот день? Решение. Число способов, которыми можно составить расписание, равно числу перестановок из шести элементов: P6=6!=1*2*3*4*5*6=720. Пример 2. Сколькими способами можно составить расписание из тех же 6 предметов, если требуется, чтобы урок физкультуры был последним? Решение. У урока физкультуры фиксированное место, поэтому расписания отличаются порядком остальных 5 предметов. Значит, число таких расписаний равно числу перестановок из 5 элементов: P5=5!= 120. Пример 3. Сколькими способами из тех же 6 предметов можно составить такое расписание, в котором русский язык и литература стоят рядом? Решение. Будем рассматривать русский язык и литературу как один предмет, тогда всего предметов будет пять. Число способов, которыми можно составить расписание из 5 предметов, равно P5=5!. Но в каждой из этих перестановок русский язык и литература могут меняться местами. Поэтому искомое число расписаний вдвое больше. Оно равно 5!*2=240. 1) в задачах на перестановки используются все элементы данного набора элементов; 2) две перестановки одного набора элементов отличаются друг от друга только порядком элементов). Задание 4 Сколькими способами можно выписать в колонку фамилии 30 учеников? Решение. P30 = 30! Задание 5 Сколько различных 5-значных чисел, все цифры которых различны можно записать с помощью цифр 4, 5, 6, 7, 8?Решение. Задача сводится к подсчету числа перестановок из 5 элементов. P5 = 1*2*3*4*5 = 120. Ответ: 120 различных чисел. Задание 6 Сколькими способами можно расставить на полке 8 книг, если среди них 2 книги одного автора, которые при любых перестановках должны стоять рядом?Решение: первоначально будем считать 2 книги одного автора единой книгой. Тогда количество способов расстановки условных семи книг на полке будет равно числу перестановок из 7 элементов: P7 = 1*2*3*4*5*6*7 = 5040. Но в каждой такой перестановке книги одного автора можно менять местами, потому общее число способов расстановки книг на полке будет в 2 раза больше, т.е. 5040 * 2 = 10080. Ответ: 10080 способов.(стр. 47 МШ - 3 - 2003). Задание 7 У Атоса, Портоса и Арамиса на всех имеется одна шпага, один кинжал и один пистолет. Сколько у них способов распределить оружие так, чтобы все были вооружены?Решение. Мушкетёров выстроим в шеренгу и отдадим каждому один из видов оружия. Тогда из шпаги, кинжала и пистолета необходимо составить различные перестановки, т. е. P3 = 3! = 1 = 6. Задание 8. Четыре лектора должны прочитать по одной лекции. Сколько имеется вариантов составления расписания? Решение. P4 = 4! = = 24 Задание 9. Капитан Жеглов рассматривает фотографии. Всего их у него 25. Сколько существует различных последовательностей их рассматривания? Решение. P25 = 25! Задание 10 У мамы есть один апельсин, одна груша, одно яблоко и один банан. Она хочет раздать их четверым детям так, чтобы каждому достался какой-нибудь фрукт. Сколько имеется вариантов это сделать? Решение. P4 = 4!=24.
|

 обычно трактуемый как биекция на множестве,
обычно трактуемый как биекция на множестве,  которая числу i ставит соответствие i-й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово расстановка.
которая числу i ставит соответствие i-й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово расстановка.
 Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают
Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают 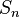
 сопоставляется с перестановкой
сопоставляется с перестановкой  , задаваемой тождеством
, задаваемой тождеством  где g — произвольный элемент группы G, а — групповая операция.
где g — произвольный элемент группы G, а — групповая операция.