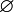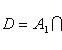Множество и подмножество. Пустое множество. Конечные и бесконечные множества. Объединение, пересечение и разность множеств. Примеры.
Множество и подмножество. Пустое множество. Конечные и бесконечные множества. Объединение, пересечение и разность множеств. Примеры. Множество — одно из ключевых понятий математики, в частности, теории множеств и логики. Математика — наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов. Теория множеств — раздел математики, в котором изучаются общие свойства множеств. Логика — наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Понятие множества обычно принимается заодно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит, и не имеющее определения. Однако, можно дать описание множества, например, в формулировке Георга Кантора: Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M). Другая формулировка принадлежит Бертрану Расселлу: «Множество есть совокупность различных элементов, мыслимая как единое целое». Также возможно косвенное определение через аксиомы теории множеств. В математической логике и дискретной математике часто употребляемый синоним множества — алфавит. Множество может быть замкнутым и незамкнутым, полным и пустым, упорядоченным и неупорядоченным, счётным и несчётным, конечным и бесконечным. Более того, как в наивной, так и в формальной теориях множеств любой объект обычно считается множеством.
Элемент множества. Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а ∉ А (а не принадлежит А). В отличие от мультимножества каждый элемент множества уникален, и в множестве не может быть двух идентичных элементов. Иначе говоря, добавление к множеству элементов, идентичных уже принадлежащим множеству, не меняет его: {6, 11} = {11, 6} = {11, 11, 6, 11, 6} Математическое понятие множества элементов принимается в качестве интуитивного. Множество задается правилом или признаком, согласно которому определяем, принадлежит ли данный элемент множеству или не принадлежит. Множество обозначают символом A = {x}, где x - общее наименование элементов множества A. Часто множество записывают в виде A = {a, b, c,...}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями: N - множество всех натуральных чисел; Z - множество всех целых чисел; Q - множество всех рациональных чисел; R - множество всех действительных чисел; C - множество всех комплексных чисел; Z0 - множество всех неотрицательных целых чисел. Аксиоматическая теория множеств Особенностью аксиоматического подхода является отказ от представления о действительном существовании множеств в некотором идеальном мире. В рамках аксиоматических теорий множества «существуют» исключительно формальным образом, и их «свойства» существенно зависят от выбора аксиом. Этот факт всегда являлся мишенью для критики со стороны тех математиков, которые не соглашались (как на том настаивал Гильберт) признать математику лишённой всякого содержания игрой в символы. В частности, Н. Н. Лузин писал, что «мощность континуума, если только мыслить его как множество точек, есть единая некая реальность», место которой в ряду кардинальных чисел не может зависеть от того, признаётся ли в качестве аксиомы континуум-гипотеза, или же её отрицание.На самом деле, вопрос выбора аксиом в данном случае тождественен выбору наших пожеланий к некоторому множеству. А выбор пожеланий — фундаментальный вопрос любого творчества. Так мы подходим к вопросу места желаний в существовании конкретной формы, удовлетворяющей желанию. Что было раньше: курица или яйцо? Так называемая объективность существования объекта (то есть вне нашего представления о нём и отношения к нему) совершенно не означает, что этот объект не был кем-то создан. Скорее, наоборот, у каждого объекта или формы есть свой творец. Значит, когда-то было время, когда каждая форма была на стадии определения требований, которым она должна соответствовать. Этот процесс определения требований был субъективным, а сама форма вообще не существовала в природе, только в воображении творца. Можно задуматься о месте объективности и о том, как и откуда она возникает. Потому, следует более осмотрительно относиться к желаниям вообще (аксиомам на языке математики). Желания иногда осуществляются, это более серьёзно, чем игра математиков с числами (аксиомами).В настоящее время наиболее распространённой аксиоматической теорией множеств является ZFC — теория Цермело — Френкеля с аксиомой выбора. Вопрос о непротиворечивости этой теории (а тем более — о существовании модели для неё) остаётся не решённым.Не всеми математиками аксиома выбора принимается безоговорочно. Так, например Эмиль Борель и Анри Лебег считают, что доказательства, полученные при помощи этой аксиомы, имеют другую познавательную ценность, чем доказательства, независимые от неё. Другие же математики, такие как Феликс Хаусдорф и Адольф Френкель, принимают аксиому выбора безоговорочно, признавая за ней ту же степень очевидности, что и за другими аксиомами Цермело — Френкеля. Подмножество в теории множеств — это понятие части множества. Определение Множество является подмножеством множества, если любой элемент, принадлежащий, также принадлежит. Формальное определение: Множество называется надмно́жеством множества, если — подмножество. Множество B, все элементы которого принадлежат множеству A, называется подмножеством множества A, и при этом записывают
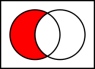
Пустое множество (в математике) — множество, не содержащее ни одного элемента. Из аксиомы объёмности следует, что есть только одно множество, обладающее таким свойством. Пустое множество является своим (тривиальным) подмножеством, но не является своим элементом.Пустое множество является конечным множеством и имеет наименьшую мощность среди всех множеств. Пустое множество — единственное множество, для которого класс множеств, равномощных ему, состоит из единственного элемента (самого́ пустого множества). Также, пустое множество — единственное множество, имеющее ровно 1 подмножество (само себя), и единственное множество, равномощное любому своему подмножеству.Пустое множество тривиальным образом является разрешимым (а значит, перечислимым и арифметическим), транзитивным (англ.) и вполне упорядоченным множеством (для любого отношения порядка). Пустое множество является наименьшим порядковым числом и наименьшим кардинальным числом. В топологии, пустое множество является одновременно замкнутым и открытым множеством. Конечные и бесконечные множества. Подмножество Для дальнейшего изучения множеств попытаемся дать некоторую их классификацию. Прежде всего, множества можно разделить на конечные и бесконечные.Конечным множеством называется множество, состоящее из конечного числа элементов. Примерами конечных множеств могут быть множество корней алгебраического уравнения n-й степени, множество букв русского алфавита, множество персонажей романа Михаила Булгакова «Мастер и Маргарита», множество атомов Солнечной системы. Причем неважно, известно число элементов множества или нет, главное, чтобы оно существовало. В математике приходится сталкиваться и с другими – неконечными, или, как принято говорить, с бесконечными множествами. Множество называется бесконечным, если оно состоит из бесконечного числа элементов. Таковы, например, множество всех натуральных чисел, множество точек окружности, множество прямых, проходящих через точку плоскости, и т.д.К конечным множествам относится и множество, не содержащее элементов вообще. Такое множество называют пустым и обозначают Æ. Необходимость его введения вызвана тем, что, определяя множество с помощью некоторого условия, мы не всегда можем сказать заранее, содержит ли оно элементы или нет. Например, в 101-й группе может не быть отличников и тогда А={а | а – отличник 101-й группы}=Æ. Пустым множеством является и множество корней системы уравнений. Без введения пустого множества мы не могли бы, скажем, говорить о множестве корней произвольного уравнения, не убедившись предварительно, что данное уравнение имеет хотя бы один корень. Существование этого понятия сокращает и упрощает формулировки многих теорем, облегчает введение новых понятий.Если каждый элемент множества В является также и элементом множества А, то говорят, что множество В называется подмножеством множества А.Обозначатся это следующим образом: В Í А (В включено в А). Например, {2, 4} Í {2, 3, 4, 5}. Множество пешек в шахматах является подмножеством шахматных фигур, множество квадратов – подмножеством прямоугольников, множество отличников 101 группы – подмножеством студентов этой группы. Подмножество В может и совпадать с множеством А, т.е. множества А и В будут состоять из одних и тех же элементов. В этом случае множества А и В называются равными: А=В (интуитивный принцип объемности). Например, множества X={2, 3} и Y={y | } состоят из чисел 2 и 3. Значит X=Y. Если в множествах А и В отличаются хотя бы одним элементом, то А¹В.Можно заметить, что само множество А является подмножеством самого себя: А Í А. (2.1) Действительно, по определению подмножества каждый элемент множества А является элементом множества А. Это свойство множества называют рефлексивностью.Кроме того, пустое множество, по определению, считают подмножеством любого множества:Æ Í А. (2.2)В самом деле, если Æ не является подмножеством А, то в нем находится хотя бы один элемент, не содержащийся в множестве А. Но в Æ такого элемента нет, так как Æ не содержит ни одного элемента.Все множества, с которыми имеют дело в том или ином рассуждении, являются подмножествами некоторого множества I, т.е. для любого множества А А Í I.В этом случае множество I называют универсальным множеством. Например, для алгебры универсальным множеством является множество действительных чисел. Если мы рассматриваем множества точек на плоскости, то универсальным будет множество всех точек на плоскости.Таким образом, у любого множества обязательно существуют хотя бы два подмножества: пустое множество и само множество. Эти два подмножества называются несобственными подмножествами. Любое подмножество, отличное от несобственного, называется собственным подмножеством данного множества.Множество всех подмножеств множества А называется множеством-степенью множества А и обозначается P(A). Например, для А={2, 3} множество-степень P(A)={А, {2}, {3}, Æ}, для А={1,2,3} множество-степень таково: P(A)={А, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, Æ}. Название «множество-степень» исходит из того, что число всех подмножеств n-элементного множества равно. Продемонстрируем данный результат. Множество, состоящее из одного элемента а, имеет два подмножества: Æ и {a}. Множество, состоящее из двух элементов а и b, имеет уже 4 подмножества: те же Æ и {a} и еще {b}, {a, b}. Добавим третий элемент с. Множество {a, b, c} кроме рассмотренных выше 4 подмножеств Æ, {a}, {b}, {a, b} имеет еще 4 подмножества {c}, {a, c}, {с, b}, {a, b, c}.Таким образом, ясно, что каждый раз прибавление еще одного элемента ведет к удвоению числа подмножеств. И множество, состоящее из n-элементов, имеет подмножеств.Кроме свойств (2.1) и (2.2) выделяют следующие свойства отношения включения: · если АÍВ и ВÍС, то АÍС (транзитивность);· если АÍВ и ВÍА, то А=В. (2.3)Для выражения (2.3) верно и обратное ему: если А=В, то АÍВ и ВÍА. Эти выражения непосредственно вытекают из определений подмножества и равенства множеств.Множество А называется истинным подмножеством множества В, если АВ и А≠В. В этом случае записывают:АÌВ.Так, {2, 4} Ì {2, 3, 4, 5}. Множество пешек в шахматах также будет истинным подмножеством шахматных фигур, а вот множество отличников 101-й группы может, чисто теоретически, совпадать с множеством студентов 101-й группы. Для истинных подмножеств также выполняется свойство транзитивности: если АВ и ВС, то АС. Операции над множествами Объединением множеств A и B называется множество элементов, принадлежащих по крайней мере одному из данных множеств (т. е. либо A, либо B, либо одновременно и A и B). Обозначают и читают "объединение A и B".Пересечением множеств A и B называется множество элементов, принадлежащих одновременно и A и B. Обозначают и читают "пересечение A и B".Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают A\B и читают "разность A и B".Пример 1. Пусть A есть отрезок [1, 3], B - отрезок [2, 4]; тогда объединением будет отрезок [1, 4], пересечением - отрезок [2, 3], разностью A\B - полуинтервал [1, 2), B\A - полуинтервал (3, 4]. Пример 2. Пусть A есть множество прямоугольников, B - множество всех ромбов на плоскости. Тогда есть множество всех квадратов, A\B - множество прямоугольников с неравными сторонами, B\A - множество всех ромбов с неравными углами.Операции объединения и пересечения множеств обладают многими свойствами сложения и умножения чисел, например переместительным, сочетательным и распределительным свойствами. Понятия объединения и пересечения множеств дословно переносятся на случай более двух множеств и даже на случай любого конечного или бесконечного множества множеств. Для удобства будем называть системами такие множества, элементами которых служат другие множества. Тогда объединением множеств некоторой системы называется множество, состоящее из элементов, принадлежащих по крайней мере одному множеству данной системы. Пересечением множеств некоторой системы называется множество, состоящее из элементов, входящих во все множества данной системы. Применяются следующие обозначения. В случае конечной системы множеств A1, A2,..., An объединение S и пересечение D обозначаются:
|

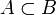


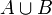


 (или
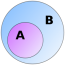
(или  )Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли" — так описал понятие "множество" Георг Кантор, основатель теории множеств. Основные предпосылки канторовской теории множеств сводятся к следующему:1° Множество может состоять из любых различимых объектов.2° Множество однозначно определяется набором составляющих его объектов.3° Любое свойство определяет множество объектов, которые этим свойством обладают.Если х — объект, Р — свойство, Р(х) — обозначение того, что х обладает свойством Р, то через {х|Р(х)} обозначают весь класс объектов, обладающих свойством Р. Объекты, составляющие класс или множество, называют элементами класса или множества.Термин "множество" употребляется как синоним понятий совокупность, собрание, коллекция некоторых элементов. Так, можно говорить о:а) множестве пчёл в улье, б) множестве точек отрезка, в) множестве вершин квадрата или о множествах его сторон и диагоналей, г) множестве студентов в аудитории и т.д. В приведённых примерах в случаях а), в)-г) соответствующие множества состоят из определённого конечного числа предметов, такие множества называются конечными. Множество точек отрезка (пример б)) пересчитать невозможно, поэтому такие множества называются бесконечными. Множество, не содержащее ни одного элемента, называется пустым множеством.Наиболее простая форма задания множества - перечисление его элементов, например А={4, 7, 13} (множество А состоит из трёх элементов - целых чисел 4, 7, 13). Другая часто применяемая форма задания - указание свойств элементов множества, например A = {x| x^2 ≤ 4} - множество чисел х, удовлетворяющих указанному условию.Множества обычно обозначаются большими буквами А, В, С,…., а их элементы - малыми: а, в, с,… Запись а ∈ А (читается: а принадлежит А) или A ∋ a (читается: А содержит а) означает, что а есть элемент множества А. Пустое множество обозначается значком Ø.Если каждый элемент множества В является также элементом множества А, множество В называется подмножеством множества А (обозначение - B ⊆ A или A ⊇ B). Каждое множество является своим подмножеством (это самое "широкое" подмножество множества). Пустое множество является подмножеством любого множества (это самое "узкое" подмножество). Любое другое подмножество множества А содержит хотя бы один элемент множества А, но не все его элементы. Такие подмножества называются истинными, или собственными подмножествами. Для истинных подмножеств множества А применяется обозначение B ⊂ A или A ⊃ B. Если одновременно B ⊆ A и A ⊆ B, т.е каждый элемент множества В принадлежит А, и в то же время каждый элемент А принадлежит В, то А и В, очевидно, состоят из одних и тех же элементов и, следовательно, совпадают. В этом случае применяется знак равенства множеств: A = B. (Символы ∈, ∋, ⊂, ⊃, ⊆, ⊇ называются символами включения).Геометрически множества обычно изображаются как некоторые множества точек плоскости. В любой имеющей смысл задаче обычно рассматриваются подмножества некоторого "наибольшего" множества U, которое называют универсальным множеством. Так, на рис. 1 изображено универсальное множество U и два его подмножества - множества А и В, B ⊂ A. Сами картинки типа рис. 1 называются диаграммами Эйлера-Венна.
)Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли" — так описал понятие "множество" Георг Кантор, основатель теории множеств. Основные предпосылки канторовской теории множеств сводятся к следующему:1° Множество может состоять из любых различимых объектов.2° Множество однозначно определяется набором составляющих его объектов.3° Любое свойство определяет множество объектов, которые этим свойством обладают.Если х — объект, Р — свойство, Р(х) — обозначение того, что х обладает свойством Р, то через {х|Р(х)} обозначают весь класс объектов, обладающих свойством Р. Объекты, составляющие класс или множество, называют элементами класса или множества.Термин "множество" употребляется как синоним понятий совокупность, собрание, коллекция некоторых элементов. Так, можно говорить о:а) множестве пчёл в улье, б) множестве точек отрезка, в) множестве вершин квадрата или о множествах его сторон и диагоналей, г) множестве студентов в аудитории и т.д. В приведённых примерах в случаях а), в)-г) соответствующие множества состоят из определённого конечного числа предметов, такие множества называются конечными. Множество точек отрезка (пример б)) пересчитать невозможно, поэтому такие множества называются бесконечными. Множество, не содержащее ни одного элемента, называется пустым множеством.Наиболее простая форма задания множества - перечисление его элементов, например А={4, 7, 13} (множество А состоит из трёх элементов - целых чисел 4, 7, 13). Другая часто применяемая форма задания - указание свойств элементов множества, например A = {x| x^2 ≤ 4} - множество чисел х, удовлетворяющих указанному условию.Множества обычно обозначаются большими буквами А, В, С,…., а их элементы - малыми: а, в, с,… Запись а ∈ А (читается: а принадлежит А) или A ∋ a (читается: А содержит а) означает, что а есть элемент множества А. Пустое множество обозначается значком Ø.Если каждый элемент множества В является также элементом множества А, множество В называется подмножеством множества А (обозначение - B ⊆ A или A ⊇ B). Каждое множество является своим подмножеством (это самое "широкое" подмножество множества). Пустое множество является подмножеством любого множества (это самое "узкое" подмножество). Любое другое подмножество множества А содержит хотя бы один элемент множества А, но не все его элементы. Такие подмножества называются истинными, или собственными подмножествами. Для истинных подмножеств множества А применяется обозначение B ⊂ A или A ⊃ B. Если одновременно B ⊆ A и A ⊆ B, т.е каждый элемент множества В принадлежит А, и в то же время каждый элемент А принадлежит В, то А и В, очевидно, состоят из одних и тех же элементов и, следовательно, совпадают. В этом случае применяется знак равенства множеств: A = B. (Символы ∈, ∋, ⊂, ⊃, ⊆, ⊇ называются символами включения).Геометрически множества обычно изображаются как некоторые множества точек плоскости. В любой имеющей смысл задаче обычно рассматриваются подмножества некоторого "наибольшего" множества U, которое называют универсальным множеством. Так, на рис. 1 изображено универсальное множество U и два его подмножества - множества А и В, B ⊂ A. Сами картинки типа рис. 1 называются диаграммами Эйлера-Венна.
 - цепочка, начинающаяся с произвольного множества, каждый последующий член которой является элементом предыдущего, всегда через конечное число шагов завершается пустым множеством (см. аксиому регулярности). Таким образом, пустое множество является «строительным кирпичиком», из которого строятся все остальные множества. В некоторых формулировках теории множеств существование пустого множества постулируется (см. аксиому пустого множества), в других — доказывается.Обозначения пустого множества - Обычно пустое множество обозначают одним из следующих символов:
- цепочка, начинающаяся с произвольного множества, каждый последующий член которой является элементом предыдущего, всегда через конечное число шагов завершается пустым множеством (см. аксиому регулярности). Таким образом, пустое множество является «строительным кирпичиком», из которого строятся все остальные множества. В некоторых формулировках теории множеств существование пустого множества постулируется (см. аксиому пустого множества), в других — доказывается.Обозначения пустого множества - Обычно пустое множество обозначают одним из следующих символов: