Элементы линейной алгебры
Матрица – прямоугольная таблица каких-либо эл-тов (чисел, мат выражений), состоящая из m-строк и n-столбцов. Если m=n, то матрица наз квадратной. Матрица состоящая из одного числа, отождествляется с этим числом. Матрица mn, все эл-ты которой равны нулю, наз нулевой матрицей и обозн через 0. Матрица, состоящая из одной строки или одного столбца, наз соотв вектор-строкой или вектор-столбцом.
Умножение матриц. Умножением матрицы А размеров m*n на матрицу В размеров n*k называется матрица С размером m*k, эл-ты которой вычисл по формуле: Свойства опер умнож матриц: Ассоциативность умножения: АВ(С)=А(ВС); Дистрибутивность умножения: А(В+С)=АВ+АС; (А+В)С=АС+ВС ЕА=А, АЕ=А, где Е – единичная матрица соответствующего порядка
Минором Алгебраическим дополнением
Определителем наз число равное разности произведений эл-тов, стоящих на главной диагонали и эл-тов, стоящих на побочной диагонали. Свойства определителей: Полилинейность – означает, что определитель линеен по всем строкам (столбцам). При добавлении линейной комб опред не изменится. Если две строки/столбца матрицы совпадают, то ее определитель равен нулю Если 2 или более строки/столбца матрицы линейно зависимы, то ее определитель равен 0.
Матрица наз вырожденной, если ее определитель равен нулю и невырожденной, если определитель матрицы отличен от нуля.
Формула вычисления обратной матрицы:
Алгоритм вычисления обратной матрицы: Пусть А – исходная матрица, обратную к которой мы хотим найти. n и k – кол-во строк и столбцов в ней соответственно Сначала проверим явл ли А квадратной, т. Е. совпадают ли nи k. Затем проверим равен ли определитель матрицы А нулю. Если он равен нулю, то обратной матрицы не существует. Создаем матрицу Inv равную единичной размерности n*n. При помощи элементарных преобразований: сложения строк матрицы, умножения строки на число, перестановки столбцов и строк приводим матрицу А к единичной. Причем, параллельно, те же преобразования производим и с матрицей Inv = > будет явл обратной матрицей к исходной А.
|

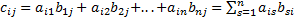 , где i=1,…,m; j=1,…,k. Умножение матриц – некоммутативная операция => сущ такие матрицы А и В, что АВ=/ВА
, где i=1,…,m; j=1,…,k. Умножение матриц – некоммутативная операция => сущ такие матрицы А и В, что АВ=/ВА (АВ)=(
(АВ)=(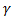 А)В=А(
А)В=А(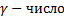
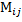 эл-та
эл-та  матрицы n-ого порядка наз определитель матрицы
матрицы n-ого порядка наз определитель матрицы  -ого порядка, полученный из матрицы А вычеркиванием i-строки и j-столбца.
-ого порядка, полученный из матрицы А вычеркиванием i-строки и j-столбца.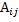 эл-та
эл-та  , где
, где 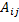 – алгебраическое дополнение эл-тов
– алгебраическое дополнение эл-тов