Алгебра высказываний
Высказывание – это утверждение, которому всегда можно поставить в соответствие одно из двух лог знач: «ложь» или «истина».
Операции над высказываниями: Отрицание – лог выск, принимает знач «истинно», если исходное высказывание ложно и наоборот. Если на входе «0», то на выходе «1» и наоборот. Конъюнкция – лог выск, истинное только тогда, когда они одновременно истинны (лог «и»). Если у обеих опер будет знач «1», то на выходе будет «1». В остальных случаях «0». Дизъюнкция – лог выск, истинное только тогда, когда хотя бы одно из них истинно (лог «или»). Если у обеих опер будет знач «0», то на выходе будет «0». В остальных случаях «1». Импликация – лог выск, ложное только тогда, когда В ложная, а А истинно. А->В и В=0 => А->В = «0». В остальных случаях «1». Эквивалентность – лог выск, истинное только тогда, когда они одновременно истинны или одновременно ложны. Если А=0 и В=0 или А=1 и В=1, то А
Составное высказывание – выск, которое образовано из простых выск путем объединения с помощью лог операций.
Классификация формул алгебры высказывания: Формула алгебры выск F( Формула алгебры выск F( Формула алгебры выск F( Формула алгебры выск F(
Основные тавтологии: Закон тождества: P Закон контрапозиции: (P Закон исключенного третьего: PVнеP
Логическая равносильность формул – ф-лы наз равносильными, если получ ф-ла тождественно истинна.
Логическое следование – одно из фундаментальных отношений между высказываниями, используемое для проверки правильности рассуждений.
Основные понятия теории вероятностей Случайное событие – подмножество множ исходов случайного эксперимента. Вероятность – Численная мера степени объективности наступления какого-либо события. Относительная частота – отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.
Совместное событие – любое событие, которое представляет собой одновременное возникновение любых двух (или более) событий. Несовместные события – несколько событий наз несовм соб, если никакие два из них не могут появиться одновременно в результате однократного испытания случ эксперимента. Полная группа событий – совокупность событий образует п.г.с. для данного испытания, если его результатом обязательно становится, хотя бы одно из них.
Свойства вероятности: Вероятность достоверного события равна единице. Вероятность невозможного события равна нулю. Вероятность случайного события есть положительное число, заключенное в промежутке между нулем и единицей.
Основные правила комбинаторики: Правило суммы: Если некоторый объект А можно выбрать n-способами, а другой объект В можно выбрать m-способами, то выбор «либо А, либо В» можно осуществить n+m-способами. Правило произведения: Если некоторый объект А можно выбрать n-способами, а после каждого такого выбора другой объект В можно выбрать m-способами, то пары объектов А и В можно выбрать n*m-способами. Сочетанием эл-тов из Е= Пересечением наз размещения без повторений из n эл-тов, в кот входят все эл-ты. Размещение из n эл-тов из Е=
|

 В будет иметь знач «1», в остальных случаях «0».
В будет иметь знач «1», в остальных случаях «0». ) наз выполнимой, если некоторая ее конкретизация явл истинным высказыванием.
) наз выполнимой, если некоторая ее конкретизация явл истинным высказыванием. Р
Р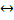 (неQ
(неQ  по k наз упорядоченное подмнож из k эл-тов, принадлежащих Е и отличающиеся друг от друга составом, но не порядком эл-тов.
по k наз упорядоченное подмнож из k эл-тов, принадлежащих Е и отличающиеся друг от друга составом, но не порядком эл-тов.


