Случайные величины
Случайной называется величина, которая в результате испытаний принимает то или иное возможное значение, за ранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств. Примеры: размер обрабатываемой детали, погрешность результата измерения какого-либо параметра изделия или среды. Два типа: дискретные и непрерывные. Дискретной наз случ величина, кринимающая конечное или бесконечное счетное множ знач. Например: частота попаданий при трех выстрелах, число брака в партии изделий. Законом распределения случайной величины наз всякое соотношение, устанавливающее связь между возможными знач случайной величины и соответствующими им вероятностями. Закон распределения дискретной случайной величины можно задать: таблично, аналитически и графически.
Числовые характеристики дискретной случайной величины: Математическим ожиданием дискретной случайной величины наз сумма произведений ее возможных знач не соответствующие им вероятности М(х)= Свойства: Мат ожид постоянной равно самой постоянной: М(с)=с Постоянный множ можно выносить за знак мат ожид: М(сх)=сМ(х) Мат ожид произведения двух независимых случ величин равно произведению их мат ожид: М(ху)=М(х)М(у) Мат ожид суммы двух случ величин (зависимых или независимых) равно сумме мат ожид слагаемых: М(х+у)=М(х)+М(у)
Дисперсией (рассеянием) случайной величины наз мат ожид квадрата ее отклонения от ее мат ожид: D(x)=M(x-M(x) Свойства: Дисперсия постоянной величины С равна нулю: D(с)=0 Постоянный множ можно выносить за знак дисперсии, возведя его в квадрат: D(cx)= Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x+y)=D(x)+D(y) Дисперсия разности двух независимых случ величин равна сумме их дисперсий: D(x-y)=D(x)+D(y)
Биноминальное распределение – это распр вероятностей возможных чисел появления соб А при n независимых испытаниях, в каждом из которых соб А можно осущ с одной и той же вероятностью P(A)=p=const. Кроме события А может произойти также противоположное событие
Непрерывной наз величина, множ знач которой заполняет сплошь некоторый числовой промежуток. Функция распределения – функ, характ распределению случ величины или случ вектора. Свойства: Не убывает: если Существуют пределы В любой точке непрерывна слева
Плотность вероятности – один из способов задания вероятностей меры на евклидовом пространстве Свойства: Плотность вероятности определена почти всюду. Если f явл плотностью вероятн Р и f(x)=g(x) почти всюду. Интеграл от плотности по всему пространству равен единице
Числовые характ непрерывных случ величин: Мат ожид непрерывной случ величины х, возможные знач которой принадлежат отрезку [a;b] наз определенный интеграл.
Нормальное распределение (распр Гаусса) – распределение вероятностей, которое задается функ плотности распр. Правило трех сигм: Пусть имеется нормально распределенная случ величина Е с мат ожид, равным а и дисперсией
|

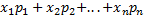

 D(x)
D(x)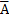 , вероятность которого Р(
, вероятность которого Р(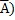 =1-р=q
=1-р=q <
< 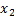 , то
, то 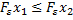
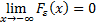 и
и 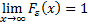
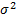 . Опред вероятность попадания Е в интервал (а-3
. Опред вероятность попадания Е в интервал (а-3 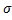 ; а+3
; а+3 


