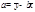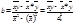Определение параметров уравнения парной регрессии.
Важнейший частный случай стат. связи – корреляционная связь. При корреляц. связи разным значениям одной переменной соответствуют различные ср. значения др. переменной, т.е. с изменением значения признака х изменяется ср. значение признака у. В статистике принято различать след. виды зависимости: 1. парная корреляция – связь между 2мя признаками результативным и факторным, либо м-ду двумя факторными. 2. частная корреляция – зависимость м-ду результативным и одним факторным признаком при фиксир. значении др. факторного признака. 3. множественная корреляция – зависимость результат. признака от двух и более факторных признаков. Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид Параметры уравнения находятся с помощью метода наименьших квадратов. Исходным методом наименьших квадратов для прямой линии является следующее:
С помощью преобразований получаем систему нормальных уравнений: an + båxi=åyi aåxi + båxi2=åxiyi Если первое уравнение системы разделить на n:
Для расчета параметра b используется формула:
Коэффициент парной регрессии, обозначенный b имеет смысл показателя силы связи между показателями факторного признака x и вариаций результативного признака y. Положительный знак при коэффициенте регрессии говорит о прямой связи между признаками, знак «-» говорит об обратной связи между признаками Важнейший частный случай стат. связи – корреляц. связь. При коррел. связи разным значениям одной переменной соответствуют различные ср. значения другой. переменной, т.е. с изменением значения признака х изменяется ср. значение признака у. Для того, чтобы определить существует или отсутствует корреляц. связь использ-ся ряд методов: Простейший способ обнаружения связи явл. сопоставление двух параллельных рядов - ряда значений факторного признака и соответств-щих ему значений результативного признака. Значения факторн. признака располагают в возраст. порядке и затем прослеживают направление изменения величины результ. признака. Пример: Если ↑ величины факт. признака влечет за собой ↑ величины результ. признака, то говорят о наличии прямой корреляц. связи. Если ↓ результ. признака- обратная связь м-ду признаками. Построение корреляц. таблицы начинают с группир-ки значений фактор. и резул. признаков. Если частоты в табл. расположены по диагонали из левого верх. угла в правый нижний- то это прямая корреляц. завис-ть м-ду признаками. Если справа-налево- то обратная связь. Графич. метод использ-ся не только для выявления связи, но и для хар-ки формы связи. Если эмпирич. линия приближается к виду прямой– прямалинейная корреляц. связь, если нет- криволин.
|

 . Где
. Где 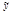 - ср. значение разультативного признака y, при определеных значениях признака x; a – свободный член уравнения; b – коэф-фициент регрессии, показывает вариацию приз-нака y, приходящуюся на единицу вариации x.
- ср. значение разультативного признака y, при определеных значениях признака x; a – свободный член уравнения; b – коэф-фициент регрессии, показывает вариацию приз-нака y, приходящуюся на единицу вариации x.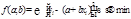
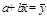 , откуда
, откуда