Частная и множественная корреляция.
Поскольку на изучаемый результат. признак влият не один факторный признак, а множество, то возникает задача изолированного измерения тесноты связи результат. признака с каждым из признаков- факторов при элиминировании (погашении связи) др. признаков-факторов, а так же задача измерения тесноты связи между результат. признаками и всеми признаками-факторами, включенными в анализ. В анализ включ-ся те фактор. признаки, для кот. их корреляция м-ду собой слабее корреляции с результат. признаком. На основе коэф-тов парной корреляции можно рассчитать коэф-ты частной корреляции. Частная корреляция- чистая корреляция м-ду двумя переменными при погашении связи с др. переменными. Коэф-т частной корреляции первого порядка, когда погашается связь с одной переменной:
Коэф-т частной корреляции второго порядка:
Точка в подстрочных значках R означает погашение связи х2 и х3 с у и х1. Коэф-ты частной корреляции принимают значения от -1 до 1. На основе коэф-тов частной корреляции расчит-ся коэф-ты частной детерминации. Он обозначается как R2(yxk.x1x2…xk-1xk+1…xm) Коэф-ты множественной детерминации показывает, какая часть дисперсии результат. переменной у объясняется за счет учтенных в анализе факторных признаков. Этот показатель обозначается R2(yx1…xk) и изменяется в интервале (0,1)
Назначение коэф-та множеств. корреляции состоит в оценке качества ур-ня множеств. регрессии: чем > значение R, тем ближе оно к 1, тем лучше уравнение регрессии, тем надежнее рез-ты анализа или прогноза на его основе.
|

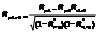
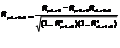
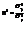 , где
, где 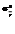 -дисперсия переменной у, а
-дисперсия переменной у, а 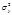 - общая дисперсия переменной у. Извлекая корень квадратный из
- общая дисперсия переменной у. Извлекая корень квадратный из 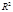 получим коэф-т множеств. корреляции у. Он должен быть не < максимального из парных или частных коэф-тов корреляции.
получим коэф-т множеств. корреляции у. Он должен быть не < максимального из парных или частных коэф-тов корреляции.


