Бинарные отношения
1. Бинарные отношения и операции над ними
ОПРЕДЕЛЕНИЕ. Пусть А1, А2,..., Аn - некоторые множества. Их прямым или декартовым произведением называется множество упорядоченных наборов из n элементов, т.е. А1´А2´... ´Аn={(а1, а2,..., аn) | aiÎAi }. Если все множества Ai совпадают A=А1=А2=... =Аn, то прямое произведение А1´А2´... ´Аn=An называют прямой n-ой степенью множества А. Бинарным отношением между элементами множеств А и В называется любое подмножество RÍA´B. Если множества A и B совпадают А=В, то R называют бинарным отношением на множестве А. Если (x, y)ÎR, то это обозначают еще xRy и говорят, что между элементами x и y установлено бинарное отношение R. Приведем примеры бинарных отношений. Пусть A=B= R, пара (x, y) является точкой вещественной плоскости. Тогда бинарное отношение R1 = { (x, y) | x2 + y2 £1 } определяет замкнутый круг единичного радиуса с центром в точке (0,0) на плоскости, отношение R2 = { (x, y) | x ³ y } полуплоскость, а отношение R3= { (x, y) | |x-y| £ 1 } полосу. Диагональ множества A´A, т.е. множество D={(x,x) | xÎA}, называется единичным бинарным отношением или отношением равенства в A. Областью определения бинарного отношения R называется множество dR={ xÎA | yÎB, (x, y) ÎR }. Областью значений бинарного отношения R называется множество rR={ yÎB | xÎA, (x, y)ÎR }. Образом множества X относительно отношения R называется множество R(X) = { yÎB | xÎX, (x, y)ÎR }; прообразом X относительно R называется R -1(X). В теории выбора и принятия решений большую роль играют бинарные отношения предпочтения, то есть такие отношения, согласно которым в паре (x, y)ÎR элемент x в каком-то смысле лучше чем y. Например: - в смысле отношения R2 "лучше" означает "больше или равно"; - в смысле отношения R3 понятие "лучше" может означать "отстоит не больше чем на единицу". Операции над бинарными отношениями определяются подобно операциям над соответствующими множествами. Пусть А – произвольное множество на котором введены бинарные отношения R, R1, R2,... 1) Объединение двух бинарных отношений R1 и R2 - это отношение R1ÈR2 = { (x, y) | (x, y)ÎR1 или (x, y)ÎR2 }. 2) Пересечение двух бинарных отношений R1 и R2 - это отношение R1ÇR2 = { (x, y) | (x, y)ÎR1 и (x, y)ÎR2 }. 3) Обратное отношение R –1 = { (x, y) | (y, x)ÎR}. 4) Дополнение к отношению 5) Двойственное отношение Rd = 6) Композиция (суперпозиция) отношений R=R1oR2 содержит пару (x, y) тогда и только тогда, когда существует такое zÎA, что (x, y)ÎR1 и (z, y)ÎR2. 7) R1 содержится в R2 (R1 Í R2), если любая пара (x, y), которая принадлежит отношению R1 также принадлежит и отношению R2.
2. Свойства операций над отношениями.
Приведем здесь список основных свойств операций над отношениями и докажем некоторые из них. 1) Ç Rk -1=(Ç Rk) -1. 2) È Rk -1=(È Rk ) -1. 3) (R1 o R2) -1 = R1 -1o R2 -1. 4) (R1 o R2 )oR3 = R1o(R2 o R3). 5) (R1 È R2 )oR3 = (R1 oR3 )È(R2o R3 ). 6) (R1 Ç R2 )oR3 Í (R1 oR3 )Ç(R2o R3 ). 7) а) если R1Í R2 то R1o R3 ÍR2o R3; б) если R1 Í R2 то R1-1Í R2-1; в) если R1 Í R2 то R3oR1 Í R3oR2. 8) a) (R1È R2)d = R1d ÇR2d; б) (R1Ç R2)d = R1d ÈR2d; в) (R d)d = R. ДОКАЗАТЕЛЬСТВО. Свойство 2. Пусть пара (x, y)Î(È Rk) -1. Тогда (y, x)ÎÈ Rk. Это означает, что найдется отношение Rj, что (y, x)Î Rj. Отсюда, по определению обратного отношения, (x, y)ÎRj-1, а значит, (x, y)ÎÈRk-1и (ÈRk)-1 Í È Rk-1. Докажем обратное включение.Пусть (x,y)Î Rk-1 Это означает, что найдется такое множество Rj, что (x,y)ÎRj-1. Следовательно, (y, x)ÎRj и (y, x)Î ÈRk ,поэтому (x, y)Î(È Rk)-1. Значит, È Rk-1 Í (ÈRk)-1. Одновременное выполнение обоих включений означает равенство множеств, что и требовалось доказать. Свойство 6. Пусть (x, y)Î(R1 ÇR2)oR3. По определению композиции это означает, что найдется такое zÎA, что (x, z)Î(R1ÇR2) и (z, y)ÎR3. Первое включение возможно только тогда, когда одновременно выполнено (x, z)ÎR1 и (x, z)ÎR2. Это, в свою очередь означает, с учетом (z, y)ÎR3, что одновременно (x, y)ÎR1oR3 и (x, y)ÎR2oR3, а, следовательно, (x, y)Î(R1oR3)Ç(R2oR3), что и доказывает требуемое соотношение. ЗАМЕЧАНИЕ. Покажем, почему неверно обратное включение. Пусть (x, y)Î(R1oR3)Ç(R2oR3), тогда (x, y) Î(R1oR3) и (x, y) Î(R2oR3). Первое включение означает существование такого элемента z1 из A, что (x, z1)ÎR1 и (z1, y)ÎR3, второе - существование такого z2ÎA, что (x, z2)ÎR2 и (z2, y)ÎR3, причем необязательно z1=z2. Значит, не всегда существует такой элемент z, что (x, z)ÎR1 и (x, z)ÎR2, а, следовательно, не будет принадлежности пересечению R1 и R2. Свойство 7б. Возьмём любую пару (x, y)ÎR1, что эквивалентно (y, х)Î ÎR1-1. Пусть теперь R1ÍR2, т.е. из (x, y)ÎR1 следует (x, y)ÎR2. Перейдя к обратным отношениям, получим, что из (y, х)ÎR1-1 вытекает (y, х)ÎR2-1, что и означает требуемое свойство. Свойство 8а. Докажем предварительно равенство (`R)-1=`R-1 Пусть (x, y)Î(`R)-1. Следовательно, (y, x) Î`R или другими словами (y, x)ÏR. Отсюда, (x, y)Ï R-1, что означает и (x, y)Î`R-1. Если же (x, y) Î`R-1, то (x, y)ÏR-1 и (y, x)ÏR. Тогда (y, x)Î`R или, что то же самое, (x,y)Î(`R)-1. Для доказательства свойства 8а воспользуемся доказанным равенством и известными свойствами операций над множествами и отношениями. _________ _______ (R1ÈR2)d = (R1ÈR2)-1 = (R1ÈR2)-1 =
=(`R1Ç`R2) =`R1-1 Ç `R2-1 = R1d Ç R2d.
3. Способы задания бинарных отношений
Традиционное задание отношений аналогично тому, как это принято в теории множеств, что не всегда удобно. Поэтому, наряду с таким заданием, применяются другие способы. 1. Матричное задание. Оно используется когда А – конечное множество А={xi}. Тогда отношение R можно задавать с помощью матрицы R={xij}, элементы которой определяются соотношением:
2. Задание с помощью графа. Для конечного множества А отношение можно задавать с помощью графа Г(R), который является геометрическим образом бинарного отношения. Граф - фигура состоящая из точек (вершин) соединенных линиями (дугами). Вершины графа соответствуют элементам множества А, то есть xi, а наличие дуги, соединяющей вершины xi и xj, означает, что (xi,xj)ÎR. Чтобы подчеркнуть упорядоченность пары на дуге ставится стрелка. Основные свойства графа. 1) Г(R-1) получается из Г(R) изменением направления стрелок на противоположные. 2) Граф Г(А´А) содержит дуги, соединяющие любую пару (xi, xj). Такой граф назывыется полным. 3. Задание верхними и нижними срезами. Этот способ может быть использован для любых множеств и отношений. Пусть на множестве А задано отношение R. Верхний срез GR (x) отношения R в точке x ÎА - это множество элементов yÎА таких, что (y, x)ÎR, т.е.
GR(x) = { yÎA | (y, x)ÎR }.
Если рассматривать R как отношение предпочтения, то GR (x) – это множество элементов, лучших чем х. Нижний срез HR(x) отношения R в точке xÎА - это множество элементов yÎА, таких, что (x, y)ÎR, т.е.
HR(x) = { yÎA | (x, y)ÎR }.
Свойства нижних и верхних срезов. Для любого хÎA и любого отношения Ri ÍA´A выполняются соотношения.
1. а) GRÇR(x)=GR(x)ÇGR(x); б) HRÇR(x)=HR(x)ÇHR(x) 2. a) G`R(x) = A\GR(x); б)H`R(x) = A\HR(x).
3. a) GR-1(x) = HR(x); б) HR-1(x) = HR(x).
4. GA´A(x) = HA´A(x) = A.
4. Свойства бинарных отношений. 1) Рефлексивность. Отношение R называется рефлексивным, если (х, х)ÎR для любого хÎA. Примеры рефлексивных отношений: отношения "³", "£" на множестве R. 2) Антирефлексивность. Отношение R называется антирефлексивным, если (х, х)ÏR для любого хÎA. Примеры антирефлексивных отношений: отношения "<", ">" на множестве R. Если R - антирефлексивное отношение, то xÏGR(x) и хÏHR(x) для любого хÎA. 3) Симметричность. Отношение R называется симметричным, если для любых x,yÎA из того, что (x, y)ÎR следует (y, x)ÎR и обратно. Примеры симметричных отношений: отношения "=" и "¹". Если отношение R симметрично, то для любого хÎA а) GR(x) = HR(x); б) R = R-1. 4) Антисимметричность. Отношение R называется антисимметричным, если для любых x и y из A из одновременного выполнения условий (x, y)ÎR и (y, x)ÎR следует, что x = y. Пример антисимметричного отношения. Пусть А - множество людей в данной очереди. Отношение R "не стоять за кем-то в очереди" будет антисимметричным. Пусть х=ВАСЯ, а y=ИВАНОВ. Тот факт, что (x, y)ÎR означает, что "ВАСЯ не стоит в очереди за ИВАНОВЫМ", (y, x)ÎR - "ИВАНОВ не стоит за ВАСЕЙ". Очевидно, что одновременное выполнение обоихвключений может быть, только если ВАСЯ и есть ИВАНОВ, т.е. x = y. Отношение "³" также антисимметрично: если x³y и y³x, то x=y. 5) Асимметричность. Отношение R асимметрично, если RÇ R-1= Æ, т.е. пересечение отношения R с обратным отношением пусто. Эквивалентное определение асимметричности: из двух отношений (x, y)ÎR и (y, x)ÎR одно не выполняется. Примеры асимметричных отношений: ">", "<", "быть начальником". Если R - асимметричное отношение, то из xRy следует yRx. Для любого отношения R вводятся понятия симметричной части отношения Rs =R ÇR-1 и асимметричной части отношения Ra = R \ Rs. Если отношение R симметрично, то R= Rs, если отношение R асимметрично, то R= Ra. Примеры. Если R - "³", то R-1 - "<", Rs - "=", Ra - ">". 6) Транзитивность. Отношение R транзитивно, если для любыx x, y, zÎA из того, что (x, y)ÎR и (y, z)ÎR следует (x, z)ÎR. Свойства транзитивного отношения: а) RoRÍR; б) для любого хÎA из yÎGR(x) следует, что GR(y)ÍGR(x). Нетранзитивным является отношение "¹". Пусть x=2, y=3, z=2, тогда справедливо x¹y и y¹z, но x=z, т.е. (x, z)ÏR. Отношение R1 называется транзитивным относительно отношения R2, если: а) из (x, y)Î R1 и (y, x)Î R2 следует, что (x, z)Î R1; б) из (x, y)Î R2 и (y, x)Î R1 следует, что (x, z)Î R1. 7) Негатранзитивность. Отношение R называется негатранзитивным, если`R транзитивно. Примеры. Отношения R1 - ">" и R2 - " ¹" негатранзитивны, так как отношения`R1 - "£",`R2 - "=" транзитивны. Возможно одновременное выполнение свойств транзитивности и негатранзитивности. Например, отношение R1 одновременно транзитивно и негатранзитивно, а R2 , как известно, транзитивным не является. 8) Полнота. Отношение R полно, если для любых x,yÎА либо (x, y)ÎR, либо (y, x)ÎR, либо оба отношения выполняются одновременно. Свойства полных отношений: а) GR(x)ÈHR(x) = А для любого хÎA; б) полное отношение рефлексивно. 9) Слабая полнота. Отношение R называется слабо полным, если для любых х¹y из А или (x, y)ÎR, или (y, x)ÎR. Пример слабо полного отношения. Пусть А - множество предприятий, "неблагополучных" в смысле своего бюджета. Отношение R "быть должным" является слабо полным, так как каждое из этих предприятий или кому-либо должно, или ему кто-то должен, но быть должным самому себе нельэя и (x, x)ÏR. 10) Ацикличность. Бинарное отношение R ациклично, если Rn ÇR-1= Æ для любого nÎ N. Иными словами, если из любой конечной цепочки отношений хRу, уRt,..., vRz следует, что z¹х, то отношение R ациклично.
9. Пусть отношения R1, R2 - симметричны. Доказать, что для того чтобы R1oR2 было симметрично необходимо и достаточно, чтобы выполнялось равенство R1oR2 = R2oR1.
5. Связи между бинарными отношениями.
1. Отношение R симметрично тогда и только тогда, когда R = R-1. 2. Если R рефлексивно, то Rd антирефлексивно, если R антирефлексивно, то Rd рефлексивно. 3. Отношение R слабо полно тогда и только тогда, когда Rd антисимметрично. ДОКАЗАТЕЛЬСТВО. Пусть R слабо полно и x¹y. Рассмотрим три случая. 1) (x, y)ÎR.Тогда, по определению обратного отношения (y,x)ÎR-1, а по определению двойственного отношения - (y,x)ÏRd. 2) (y,x)ÎR, тогда (x, y)ÎR-1 и, следовательно, (x,y)Ï`R-1 = Rd. 3) (x, y)ÎR и одновременно (y, x)ÎR. Отсюда, (y, х)ÏRd и (x, y)Ï Rd. Так как R - слабо полное отношение, то для любых x¹y выполняется либо случай а), либо б), либо в). Ни в одном из этих случаев включения (x, y)ÎRd и (y, x)ÎRd не могут выполняться одновременно. Следовательно, отношение Rd антисимметрично. Докажем, что из антисимметричности Rd следует слабая полнота отношения R. Рассмотрим эквивалентное определение антисимметричности. Если x¹y, то либо (x,y)ÎRd и (y,x)Ï Rd, либо (x,y)ÏRd и (y,x)ÎRd, либо (x,y)ÏRdи (y,x)ÏRd. В первом случае получим, что (x,y)ÎR, во втором - (y,x)ÎR, в третьем - (x,y)ÎR и (y,x)ÎR. Это утверждение означает, что отношение R слабо полно. 4. Отношение R асимметрично тогда и только тогда, когда Rd полно. ДОКАЗАТЕЛЬСТВО. Пусть R - асимметрично. Тогда по определению, RÇR-1 = Æ. Рассмотрим два случая. 1) (x, y)ÎR. Тогда (х, y)ÏR-1, значит, (x, y)ÎRd. 2) (x, y)ÏR. Тогда (x, y)Î`R и (y, x) Î`R-1 = Rd. В любом случае либо (x, y)ÎRd, либо (y, x)ÎRd, а это означает, что Rd - полно. Докажем обратное следствие. Пусть Rd полно. Снова рассмотрим два случая: а) (x, y)ÎRd, тогда (y, x)ÏR; б) (y, x)ÎRd, тогда (x, y)ÏR. Так как Rd полно, то либо случай а), либо случай б) всегда будет иметь место, а отсюда следует невозможность одновременного выполнения yRx и xRy. Это означает, что R асимметрично. Примеры решений задания № 3. Пример 1. Доказать, что если отношения R1, R2 рефлексивны, то справедливо включение R1ÈR2 Í R1oR2 .
Доказательство. Пусть (x, y)ÎR1ÈR2, тогда (x, y)ÎR1 или (x, y)ÎR2. В первом случае из рефлексивности R2 следует (y, y)ÎR2 и, следовательно, (x, y)Î R1oR2. Аналогично для второго случая получим (x, x)ÎR1 и (x, y)ÎR1oR2, что и требовалось доказать.
Пример 2. Доказать, что отношения RÈ(`RÇRd)=RÈ(`R)s полны.
Докажем равенство множеств, воспользовавшись свойствами операций над множествами и отношениями. RÈ(`R Ç Rd ) = RÈ(`R Ç`R-1) = RÈ(`RÇ(`R)-1) = =RÈ(`R)s. Покажем теперь, что отношение RÈ(`R)s полно. Для любых x, yÎA возможен один из трех случаев: 1) (x, y)ÎR; 2) (y, x)ÎR; 3) (x, y)ÏR и (y, x)ÏR. В первых двух случаях принадлежность (x,y) к рассматриваемому отношению очевидна. Рассмотрим третий случай. Так как (x,y)Î`R и (x,y)Î R-1, то (x,y)Î(`R)s. Следовательно, рассматриваемое отношение полно.
Варианты задания №1. Доказать соотношение. 0. AÇ(BÇC) = (AÇB)ÇC. 1. AÈ(BÈ C) = (AÈB)È C. 2. 3. 4. 5. 6. 7. 8. (AÈB) \ C = (A \ C) È (B \ C). 9. A \ (B Ç C) = (A \ B) È (A \ C).
Варианты задания №2. 0. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
1. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
2. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
3. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
4. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
5. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
6. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
7. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
8. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
9. a). Определить проекции б). Определить проекции множества векторов
г). Пусть д). Сравнить векторные оценки множества
Варианты задания №3. 0. Доказать, что если отношение R транзитивно, то R-1 также является транзитивным. 1. Доказать, что из асимметричности отношения R следует асимметричность R-1. 2. Доказать, что из антисимметричности отношения R следует антисимметричность R-1. 3. Доказать, что из рефлексивности отношения R следует рефлексивность R -1. 4. Доказать, что для симметричности отношения R необходимо и достаточно, чтобы Rd было симметрично. 5. Доказать, что если отношения R1 и R2 рефлексивны, то рефлексивны отношения R1ÈR2, R1ÇR2, R1-1. 6. Доказать, что если отношения R1 и R2 антирефлексивны, то антирефлексивны и отношения R1ÈR2, R1ÇR2, R1-1. 7. Доказать, что если отношения R1 и R2 симметричны, то симметричны отношения R1ÈR2, R1ÇR2, R1-1. 8. Доказать, что если отношения R1 и R2 антисимметричны, то антисимметричны также R1ÇR2 и R1-1. 9. Пусть отношения R1, R2 - симметричны. Доказать, что для того чтобы R1oR2 было симметрично необходимо и достаточно, чтобы выполнялось равенство R1oR2 = R2oR1.
|

 ={ (x, y) | (x, y)Î(A´A)\R}.
={ (x, y) | (x, y)Î(A´A)\R}. .
.

 .
. .
. .
. .
. .
. .
. , если
, если 
 :
:  , если
, если .
.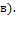 Определить проекции упорядоченного множества векторов
Определить проекции упорядоченного множества векторов  Найти
Найти  .
.
 . Найти парето-оптимальные оценки.
. Найти парето-оптимальные оценки. , если
, если 
 :
:  , если
, если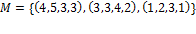 .
. Найти
Найти 
 . Найти парето-оптимальные оценки.
. Найти парето-оптимальные оценки. , если
, если 
 :
:  , если
, если .
. .
. Найти
Найти 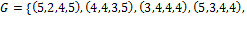
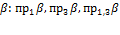 , если
, если 
 :
:  , если
, если .
. Найти
Найти 
 . Найти парето-оптимальные оценки.
. Найти парето-оптимальные оценки. , если
, если  , если
, если Найти
Найти 
 . Найти парето-оптимальные оценки.
. Найти парето-оптимальные оценки. , если
, если 
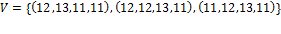 .
. Найти
Найти 
 . Найти парето-оптимальные оценки.
. Найти парето-оптимальные оценки.
 .
. Найти
Найти 
 . Найти парето-оптимальные оценки.
. Найти парето-оптимальные оценки.
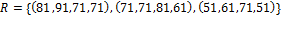 .
. .
.
 . Найти парето-оптимальные оценки.
. Найти парето-оптимальные оценки.
 .
. Найти
Найти 
 . Найти парето-оптимальные оценки.
. Найти парето-оптимальные оценки.
 .
. .
. Найти
Найти 
 . Найти парето-оптимальные оценки.
. Найти парето-оптимальные оценки.


