ФГБОУ ВО
«Воронежский государственный университет инженерных технологий» КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНоЛОГИЙ МОДЕЛИРОВАНИЯ И УПРАВЛЕНИЯ
Методические указания и задания К контрольной работе № 1 по дисциплине “ДИСКРЕТНАЯ МАТЕМАТИКА ”
для студентов 1-го курса ФБО направления 09.03.02
Воронеж 2014
Контрольная работа состоит из трех заданий. К кажому заданию приведены необходимые для их выполнения теоретические сведения и примеры выполнения заданий. Ход выполнения и результаты решения заданий студентом оформляются средствами MS WORD. Номер варианта каждого задания выбирается по последней цифре шифра логина студента. Варианты заданий приведены на стр. 23.
Теоретический материал к заданию № 1. Основные понятия теории множеств
Для множества не существует строгого определения, поэтому введем описательные понятия множества и его элементов. Множеством называется совокупность некоторых предметов, объединенных общим признаком. Элементы множества - это те предметы, из которых состоит множество. Пусть имеется множество А, элементом которого является предмет а, это записывается как А={а}. Например, В={1,2, 3}. Если какой-то элемент а принадлежит множеству А, то это обозначается аÎА, а если b не принадлежит А, то - bÏА. Например, пусть А - множество четных натуральных чисел, тогда 6ÎА, а 3ÏА. Пусть имеется два множества А и В, причем все элементы множества А принадлежат множеству В, т.е. если хÎА, то хÎB. В этом случае говорят, что множество А включено в множество В. Обозначается: АÍВ (Í - символ нестрогого включения, т.е. возможно совпадение множеств). Множество А совпадает со множеством В (А = В), если все элементы множества В являются элементами множества В и все элементы множества В являются элементами множества А. Это можно записать в виде (АÍВ и ВÍА) <=> (А = В). Множество А строго включено в множество В, если все элементы множества А принадлежат множеству В, но не все элементы множества В принадлежат множеству А. Пример: А = { 1, 2, 3 }, В = { 0, 1, 2, 3 }, АÌВ. Возможны два способа задания множества. 1. Перечислением элементов, т.е. в фигурных скобках дается полное перечисление элементов данного множества. Например: N = {1,2,...,n,...} - множество натуральных чисел. 2. С помощью указания характерного свойства (указание свойства, которым обладают только элементы данного множества). Символически это записывается в виде A={x | P(x)} и читается A есть множество всех элементов х, обладающих свойством P(x). При задании множеств вторым способом возможны различные противоречия и парадоксы. Рассмотрим примеры таких парадоксов. 1) Парадокс парикмахера: в городе жил парикмахер, который брил всех, кто не брился сам. Кто же брил парикмахера? 2) Пусть имеем натуральное число 11218321 - одиннадцать миллионов двести восемнадцать тысяч триста двадцать один. Это число можно описать с помощью восьми слов. Пусть А - множество натуральных чисел, которые нельзя определить с помощью фразы, имеющей меньше 20 русских слов. Обозначим аmin - наименьшее число из множества А, причем аminÎA. Число аmin можно определить следующим образом: наименьшее натуральное число, которое нельзя определить с помощью фразы, имеющей менее двадцати слов. В этой фразе 14 слов. Значит, аmin можно определить с помощью фразы, содержащей менее 20 слов. Тогда получается, что аminÏ А. К настоящему времени накопилось много подобных примеров, когда определение множества оказывалось внутренне противоречиво. Выяснение условий, при которых это может иметь место потребовало специальных исследований, составивших предмет математической логики и выходящих за рамки собственно теории множеств. Поэтому в данном пособии мы не станем касаться спорных случаев и будем рассматривать лишь множества, которые определяются точно и без противоречий. В теории множеств имеется специальное множество, называемое пустым множеством (Æ), которое не содержит ни одного элемента. Пустое множество по определению содержится в любом множестве А (ÆÎА). Это понятие вводится из следующих соображений. Задавая множество вторым способом не всегда заранее можно быть уверенным, существуют ли элементы, ему принадлежащие. Например, можно говорить о множестве четырехугольников на плоскости, у которых все углы прямые, а диагонали не равны. Только знания основ геометрии позволяют убедиться, что таких четырехугольников не существует и, следовательно, это множество пусто. Большинство утверждений теории множеств связано с равенством двух множеств и включением одного множества в другое. Поэтому надо детально разобраться в методах доказательства этих фактов. 1. Доказательство включения АÍВ. Для этого нужно доказать, что любой элемент x, принадлежащий множеству А одновременно является элементом множества В, т.е. (x Î А) => (x Î В). 2. Доказательство равенства А = В. Оно сводится к доказательству двух включений АÍВ и ВÍА. Пример 1. Докажем следующую теорему. Для любых множеств А, В и С выполняется закон транзитивности нестрогого включения, т.е. если АÍВ и ВÍС, то из этого следует, что АÍС. Доказательство. Пусть x - любой элемент множества А, (xÎА), тогда в силу условия АÍВ, по определению нестрогого включения, элемент х принадлежит множеству В (хÎB). После доказательства этого факта, аналогично, используя условие ВÍС можно доказать, что х принадлежит С (хÎС). В качестве исходного допущения мы приняли, что x – любой элемент из А. Из этого допущения при выполнении условий а) и б) получено следствие хÎС. По определению нестрогого включения это означает АÍС, что и требовалось доказать. Пример 2. Пусть А={1,6}, В ={х | х2-7х+6=0}. Последнее читается как, В является множеством элементов х, для которых выполняется условие х2 - 7х + 6 = 0. Включение АÍВ доказывается подстановкой элементов множества А в это условие. Для доказательства обратного включения ВÍА нужно найти все корни уравнения и убедиться, что они равны 1 и 6, т.е. принадлежат А. Выполнение обоих нестрогих включений означает равенство множеств А и В.
Операции над множествами.
Определим следующие операции. 1. Объединение. Пусть А и В - произвольные множества. Их объединением называется множество С = АÈВ, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств А или В. 2. Пересечение. Пересечением множеств А и В называется множество С, состоящее из элементов одновременно принадлежащих А и В. Обозначается так: C=AÇB. 3. Разность. Разность множеств А и В - это множество С (С=А\В), состоящее из элементов множества А, не принадлежащих множеству В. Если ВÍА, то разность С = А\В называется дополнением В до А. Иногда, говоря о некотором наборе множеств подразумевают, что все они включены в некоторое множество S, которое называют универсальным множеством. В этом случае дополнение какого-либо множества А до S обозначается С(А) или 4. Симметричная разность. По определению симметричная разность двух множеств А и В - это множество С = АDВ = (А\В)È(В\А). Основные свойства операций. 1. Операции пересечения и объединения коммутативны (перестановочны): АÇВ = ВÇА; АÈВ = ВÈА. 2. Операции пересечения и объединения ассоциативны. (АÇВ) ÇС = АÇ (ВÇС) = АÇВÇС (АÈB) ÈС = АÈ (ВÈС) = АÈВÈС. Свойствами коммутативности и ассоциативности обладают Пример некоммутативной операции - операция умножения матриц (АВ¹ВА). 3. Операции объединения и пересечения взаимно дистрибутивны. Для вещественных чисел закон дистрибутивности читается так: а(в+с) = ав + ас. Для множеств закон дистрибутивности имеет вид: а) (АÈВ)ÇС = (АÇС) È (ВÇС) б) (АÇB) ÈС = (АÈС) Ç (ВÈС). Докажем равенство а). Предположим, что xÎ (АÈВ) ÇС, тогда xÎС и xÎА или xÎВ. Рассмотрим первый случай xÎС и xÎА. Тогда хÎАÇС, а значит, по определению объединения, хÎ(АÇС)È(ВÇС). Во втором случае, т.е. при xÎС и xÎВ получаем, что xÎ (ВÇС)È(АÇС). Таким образом, мы доказали включение [(АÈВ) ÇС]Í[(АÇС)È(ВÇС)]. Докажем обратное включение. Пусть хÎ(АÇС)È(ВÇС), тогда хÎАÇС или хÎВÇС. В первом случае хÎА и хÎС. Во втором случае хÎВ и xÎС. В обоих случаях получаем, что хÎС и хÎА или хÎВ. Следовательно, хÎ(АÈВ) ÇС. Тем самым доказано включение (АÇС)È(ВÇС)Í(АÈВ) ÇС. Таким образом, (АÈВ) ÇС=(АÇС)È(ВÇС), что и требовалось доказать. Пусть А1, А2,... - некоторые множества и пусть все они включены в S (А1, А2,... Í S). Тогда выполняются следующие соотношения. 4. 5. Докажем свойство 4. Пусть хÎ Обратно, пусть хÎ
Пример решения задания № 1. Доказать соотношение AUB=AU(B\A). Чтобы доказать это соотношение, нужно показать, что каждый элемент первого множества принадлежит второму и наоборот, то есть эти множества совпадают. Пусть x∈AUB, то есть x∈A или x∈B. Если x∈A, то x∈AU(B\A). Если x∉A, но x∈B, то x∈B\A, следовательно, x∈AU(B\A). Пусть x∈AU(B\A), то есть x∈A или x∈B\А. Если x∈A, то x∈AUB. Если x∈В, но x∉A(x∈B\А), то x∈AUB. Таким образом, соотношение доказано.
|


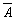 .
. многие операции. Чтобы не создалось впечатления, что коммутативность и ассоциативность являются общими свойствами всех операций, приведем пример неассоциативной операции - возведение в степень. Имеем: (23)2 = 82 = 64;
многие операции. Чтобы не создалось впечатления, что коммутативность и ассоциативность являются общими свойствами всех операций, приведем пример неассоциативной операции - возведение в степень. Имеем: (23)2 = 82 = 64;  = 28 = 512.
= 28 = 512.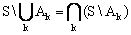 - дополнение объединения множеств равно пересечению их дополнений.
- дополнение объединения множеств равно пересечению их дополнений.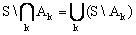 - дополнение пересечения множеств равно объединению их дополнений.
- дополнение пересечения множеств равно объединению их дополнений. , тогда хÏ
, тогда хÏ  значит, x не принадлежит ни одному из множеств Ak ("k, хÏАk), следовательно, по определению дополнения хÎS\Аk для любого k. Отсюда вытекает, что хÎ
значит, x не принадлежит ни одному из множеств Ak ("k, хÏАk), следовательно, по определению дополнения хÎS\Аk для любого k. Отсюда вытекает, что хÎ  .
.


