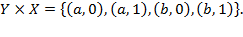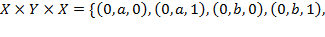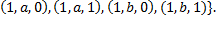Векторы, прямые произведения, произведения векторов.
Вектор  , где
, где  - компоненты (координаты) вектора. Число
- компоненты (координаты) вектора. Число  компонент называется длиной (размерностью) вектора.
компонент называется длиной (размерностью) вектора.
Два вектора  и
и 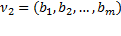 равны, если они имеют одинаковую длину и соответствующие координаты их равны, т.е.
равны, если они имеют одинаковую длину и соответствующие координаты их равны, т.е.  , если: 1).
, если: 1).  ; 2).
; 2).  .
.
Множество всех возможных (различающихся) векторов  длины
длины  таких, что
таких, что  , называют прямым произведением множеств
, называют прямым произведением множеств 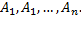 Обозначение прямого произведения:
Обозначение прямого произведения:  . Прямое произведение
. Прямое произведение  одинаковых множеств
одинаковых множеств  , т.е. когда
, т.е. когда  , обозначают
, обозначают  .
.
Мощность прямого произведения множеств  равна произведению мощностей этих множеств, т.е.
равна произведению мощностей этих множеств, т.е. 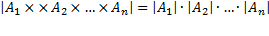 .
.
Способы задания прямого произведения множеств  - аналогичны способам задания множеств с той разницей, что требуется задание каждого множества
- аналогичны способам задания множеств с той разницей, что требуется задание каждого множества 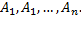
Операции над множествами векторов (данного прямого произведения) – объединение, пересечение, разность, дополнение – аналогичны соответствующим операциям над множествами элементов.
Операции над вектором  длины
длины  :
:  .
.
Проекцией вектора  на
на  ю ось называется его
ю ось называется его  я компонента:
я компонента:  .
.
Проекцией вектора  на оси с номерами
на оси с номерами  называется вектор длины
называется вектор длины  :
: 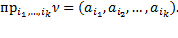
Операции над множеством векторов  длины
длины  :
:
 .
.
Проекцией множества векторов  на
на  ю ось называется множество проекций всех векторов из
ю ось называется множество проекций всех векторов из  на
на  ю ось:
ю ось:
 .
.
Проекцией множества векторов  на оси с номерами
на оси с номерами  называется множество проекций всех векторов
называется множество проекций всех векторов  на оси с номерами
на оси с номерами  :
:
 .
.
Операции над упорядоченным множеством векторов  длины
длины  :
:  .
.
Проекцией упорядоченного множества векторов  на
на  ю ось называется упорядоченное множество проекций векторов на эту ось:
ю ось называется упорядоченное множество проекций векторов на эту ось:  .
.
Проекцией упорядоченного множества векторов  на оси с номерами
на оси с номерами  называется упорядоченное множество проекций всех векторов
называется упорядоченное множество проекций всех векторов  на оси с номерами
на оси с номерами  :
:
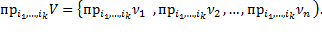
Над векторами  одинаковой длины
одинаковой длины  возможно выполнение различных операций сравнения.
возможно выполнение различных операций сравнения.
Правило сравнения векторов по предпочтению. Пусть  - множество векторов длины
- множество векторов длины  , компонентами которых являются числа. Вектор
, компонентами которых являются числа. Вектор 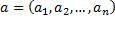 не менее предпочтителен, чем вектор
не менее предпочтителен, чем вектор  (обозначение
(обозначение  ), если компоненты вектора
), если компоненты вектора  не меньше соотвествующих компонент вектора
не меньше соотвествующих компонент вектора 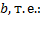
 .
.
Примеры решений задания № 2.
1). Пусть  . Определить проекции
. Определить проекции  :
:
1. на первую ось;
2. на вторую ось;
3. на вторую и третью ось.
Решение.
Проекции множества векторов  :
:
 .
.
2). Пусть  упорядоченное множество векторов. Определить проекции
упорядоченное множество векторов. Определить проекции  :
:
1. на первую ось;
2. на вторую ось;
3. на вторую и третью ось.
Решение.
Проекции упорядоченного множества векторов  :
:  .
.
3). Пусть  Найти
Найти  .
.
Решение.

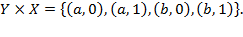

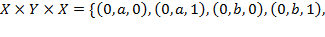
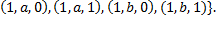

 , где
, где  - компоненты (координаты) вектора. Число
- компоненты (координаты) вектора. Число  компонент называется длиной (размерностью) вектора.
компонент называется длиной (размерностью) вектора. и
и 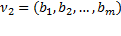 равны, если они имеют одинаковую длину и соответствующие координаты их равны, т.е.
равны, если они имеют одинаковую длину и соответствующие координаты их равны, т.е.  , если: 1).
, если: 1).  ; 2).
; 2).  .
. длины
длины  , называют прямым произведением множеств
, называют прямым произведением множеств 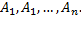 Обозначение прямого произведения:
Обозначение прямого произведения:  . Прямое произведение
. Прямое произведение  , т.е. когда
, т.е. когда  , обозначают
, обозначают  .
. равна произведению мощностей этих множеств, т.е.
равна произведению мощностей этих множеств, т.е. 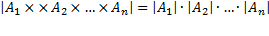 .
. - аналогичны способам задания множеств с той разницей, что требуется задание каждого множества
- аналогичны способам задания множеств с той разницей, что требуется задание каждого множества  длины
длины  .
. ю ось называется его
ю ось называется его  .
. называется вектор длины
называется вектор длины  :
: 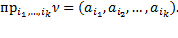
 длины
длины  .
. .
. на оси с номерами
на оси с номерами  .
. .
. .
.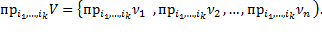
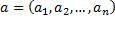 не менее предпочтителен, чем вектор
не менее предпочтителен, чем вектор  (обозначение
(обозначение  ), если компоненты вектора
), если компоненты вектора  не меньше соотвествующих компонент вектора
не меньше соотвествующих компонент вектора 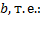
 .
. . Определить проекции
. Определить проекции  .
. .
. Найти
Найти  .
.