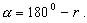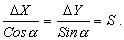Румбы. Связь румбов с дирекционными углами.
румбом называется острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб. Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам: I четверть (СВ) r = α II четверть (ЮВ) r = 180° – α III четверть (ЮЗ) r = α – 180° IV четверть (СЗ) r = 360° – α Румб в точке М направления ВС называется прямым, а противоположного направления СВ – обратным. Прямой и обратный румб в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей. 19. Прямая геодезическая задача В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние SAB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол αAB или румб rAB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.
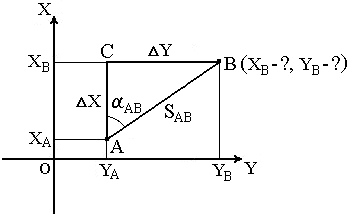
Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом. Дано: Точка А(XA, YA), SAB и αAB. Найти: точку В(XB, YB). Непосредственно из рисунка имеем: ΔX = XB – XA; ΔY = YB – YA. Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС: ΔX = SAB · cos αAB;ΔY = SAB · sin αAB. Так как в этих формулах SAB всегда число положительное, то знаки приращений координат ΔX и ΔY зависят от знаков cos αAB и sin αAB. При помощи румба приращения координат вычисляют по формулам: ΔX = SAB · cosrAB;ΔY = SAB · sin rAB. Знаки приращениям дают в зависимости от названия румба. Вычислив приращения координат, находим искомые координаты другой точки: XB = XA + ΔX; YB = YA + ΔY. Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения. Контроль вычислений координат выполняют по формуле 20. Обратная геодезическая задача Обратная геодезическая задача – это вычисление дирекционного угла α и длины S линии, соединяющей два пункта с известными координатами X1, Y1 и X2, Y2
Построим на отрезке 1-2 как на гипотенузе прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна S, катеты равны приращениям координат точек 1 и 2 (ΔX = X2 – X1, ΔY = Y2 – Y1), а один из острых углов равен румбу r линии 1-2. Если Δ X 00 и Δ Y 00, то решаем треугольник по известным формулам:
Общий порядок нахождения дирекционного угла линии 1-2 включает две операции: * определение номера четверти по знакам приращений координат Δ>X и ΔY (рис.1.4-а), * вычисление α по формулам связи (1.22) в соответствии с номером четверти.Контролем правильности вычислений является выполнение равенства: Контроль: d. cos α + XA = XB, d. sin α + YB = YB. План. Карта и профиль. На картах изображают обычно поверхность всей Земли или ее частей. С геометрической точки зрения карта представляет более или менее искаженное изображение земной поверхности. Это объясняется тем, что сферическую поверхность земли невозможно изобразить на бумаге без искажений. Поэтому при построении карт пользуются различными картографическими проекциями, в которых по определенному математическому закону сначала строят географическую сетку меридианов и параллелей, а затем по ней наносят детали местности. Чем больше изображаемая на карте территория, тем с большими искажениями получают на карте объекты. С этой точки зрения картой называют уменьшенное, построенное в картографической проекции, обобщенное изображение поверхности Земли. Если для построения карты точки и линии местности проецируют нормалями на поверхность эллипсоида, а затем поверхность эллипсоида по определенным математическим законам изображают на плоскости, то для построения плана точки и линии местности проецируют перпендикулярами(ортогонально) на горизонтальную плоскость и полученное на ней горизонтальное проложение участка земной поверхности уменьшают в определенное число раз с сохранением подобия фигур, полученных на горизонтальной плоскости. План – это уменьшенное подобное изображение на плоскости горизонтального проложения участка земной поверхности. Его нельзя составить на очень большую территорию, т.к. кривизна земли вызовет большую разницу между горизонтальными проложениями линий местности и их проекциями на поверхность эллипсоида. К геодезическим материалам относят профиль местности, т.е. уменьшенное изображение вертикального разреза земной поверхности. На нем линию, изображающую уровенную поверхность, проводят обычно в виде прямой. Разрез местности представляет обычно кривую линию, а профиль строят в виде ломаной линии, и поворотные точки линии представляют характерные точки местности, высоты которых определяют либо по карте, либо по измерениям на местности. Условные знаки планов и карт. Топографические условные знаки принято разделять на масштабные (или площадные), внемасштабные, линейные и пояснительные. Масштабные, или площадные условные знаки служат для изображения таких топографических объектов, занимающих значительную площадь и размеры которых в плане могут быть выражены в масштабе данной карты или плана. Площадной условный знак состоит из знака границы объекта и заполняющих его знаков или условной окраски. Внемасштабные условные знаки используются для передачи объектов, не выражающихся в масштабе карты. Эти знаки не позволяют судить о размерах изображаемых местных предметов. Положению предмета на местности соответствует определенная точка знака. Линейные условные знаки предназначены для изображения протяженных объектов на местности, например железные и автомобильные дороги, просеки, линии электропередач, ручьи, границы и другие. Они занимают промежуточное положение между масштабными и внемасштабными условными знаками. Пояснительные условные знаки применяются в целях дополнительной характеристики показываемых на карте местных предметов. Например, длина, ширина и грузоподъемность моста, ширина и характер покрытия дорог, средняя толщина и высота деревьев в лесу, глубина и характер грунта брода и т. д.
|

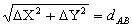
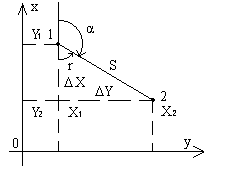

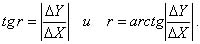 Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому на основании (1.22) находим:
Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому на основании (1.22) находим: