Предложение и производственная функция. Спрос на произведенную продукцию и функция потребления. Устойчивый уровень капиталовооруженности. Приближение к устойчивому состоянию.
Предложение и производственная функция. Предложение товаров в модели Солоу описывается с помощью произв. ф-ции: Y = F(K,L). Модель роста Солоу предполагает, что произв. ф-ция обладает свойством постоянной отдачи от масштаба. Это выполняется, если zY = F(zK, zL), для любого z > 0. Cоотнесем все величины с кол-вом работников. Произв. ф-ция с пост. отдачей от масштаба удобна для этой цели потому, что объём про-ва на 1 рабочего зависит только от кол-ва К, приходящегося на 1 рабочего. Примем z = 1/L, тогда Y/L = F(K/L, 1). Это ур-ие показывает, что объём про-ва в расчёте на 1 работника (Y/L) является функцией К на 1 работника (K/L). Используем малые буквы для колличественных показателей, которые относятся к 1 рабочему: у = Y/L - выпуск продукции на 1 работника или производительность труда, a k = K/L - К, приходящийся на 1 работника или капиталовооруженность труда. Тогда произв. ф-ция: У = f(k), где f(k) = F(k,l). Используя произв. ф-цию, соотносящую производительность труда с капиталовооруженностью, мы упрощаем анализ.
По мере роста капиталовооруженности график произв. ф-ции становится более пологим, т.е. угол наклона уменьшается. Такая произв. ф-ция характеризуется понижающейся предельной производительностью К: каждая дополнительная ед. К производит меньше продукта, чем предыдущая. Когда запас К на 1 работника невелик, каждая дополнительная единица К дает большую отдачу. Если капиталовооруженность высокая, то дополнительная ед. К менее эффективна. Спрос на произведенную продукцию и функция потребления.В модели Солоу спрос на товары предъявляется со стороны потребителей и инвесторов. Т.е., у = с + i. Это уравнение сходно с тождеством национальных счетов. Модель Солоу предполагает, что ф-ция потребления принимает форму: с = ( 1- s) * y, где норма сбережения s от 0 до 1. Эта ф-ция означает, что потребление пропорционально доходу. Каждый год часть (1-s) дохода потребляется и часть s сберегается. Заменим с на (l-s)y в тождестве национальных счетов: у = ( l -s)y + i. Отсюда i = sy. Это уравнение показывает, что i (как и c) пропорциональны y. Если i = s, норма сбережений s также показывает, какая часть произведенной продукции направляется на капитальные вложения. Устойчивый уровень капиталовооруженности. Запасы К могут изменяться по двум причинам: 1) i приводят к росту запасов К. 2) Часть К амортизируется, что приводит к уменьшению запасов К.
Чтобы учесть амортизацию, предположим, что ежегодно выбывает определенная доля К б - норма выбытия. Кол-во К, которое выбывает каждый год = б* k. На рис.2 показано, как выбытие зависит от запасов К.
На рис. 3 i и выбытие показаны для различных уровней капиталовооруженности k. Чем выше k, тем больше объем производства и i, приходящиеся на 1 работника. Однако, чем больше запасы К, тем больше и величина выбытия. Сущ. единственный уровень k, при котором i = выбытию. При данном уровне k, ∆k=0. Назовем это состоянием устойчивой капиталовооруженности и обозначим его k *. Приближение к устойчивому состоянию. Независимо от первоначального объёма капитала, с которым экономика начинает развиваться, она затем достигает устойчивого состояния. Если k<k*, то i > выбытие. Т.о., k увеличивается и будет расти вместе с производством, пока не приблизится к устойчивому уровню k*. При k>k* i < выбытия, К выбывает быстрее, чем добавляется. Т.о., k будет сокращаться, приближаясь к k*. В момент, когда запасы К, приходящиеся на 1 работника, достигнут устойчивого уровня, i сравняются с выбытием, и k не будет ни расти, ни падать.
|

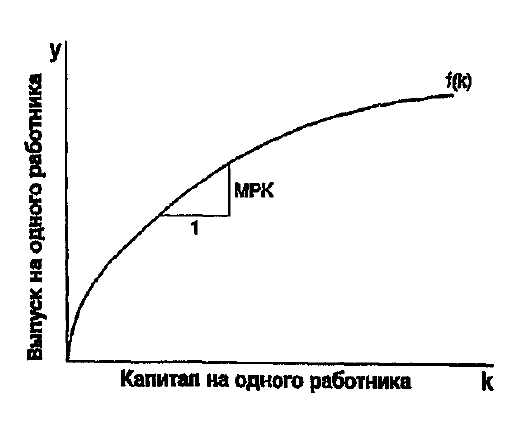 Тангенс угла наклона производственной функции показывает, сколько дополнительного продукта на 1 работника можно получить, если увеличить капиталовооруженность на 1 ед.. Эта величина является предельным продуктом капитала МРК. МРК = f(k+l)-f(k).
Тангенс угла наклона производственной функции показывает, сколько дополнительного продукта на 1 работника можно получить, если увеличить капиталовооруженность на 1 ед.. Эта величина является предельным продуктом капитала МРК. МРК = f(k+l)-f(k).
 i в расчёте на 1 работника являются частью продукта, приходящегося на 1 работника (sy). Заменив у выражением произв. ф-ции, мы представим i на 1 работника как ф-цию от капиталовооруженности: i = sf(k). Чем выше уровень капиталовооруженности k, тем выше объем производства f(k) и больше i. На рис.1 показано, как норма сбережений определяет разделение продукта на c и i для каждого из значений k.
i в расчёте на 1 работника являются частью продукта, приходящегося на 1 работника (sy). Заменив у выражением произв. ф-ции, мы представим i на 1 работника как ф-цию от капиталовооруженности: i = sf(k). Чем выше уровень капиталовооруженности k, тем выше объем производства f(k) и больше i. На рис.1 показано, как норма сбережений определяет разделение продукта на c и i для каждого из значений k.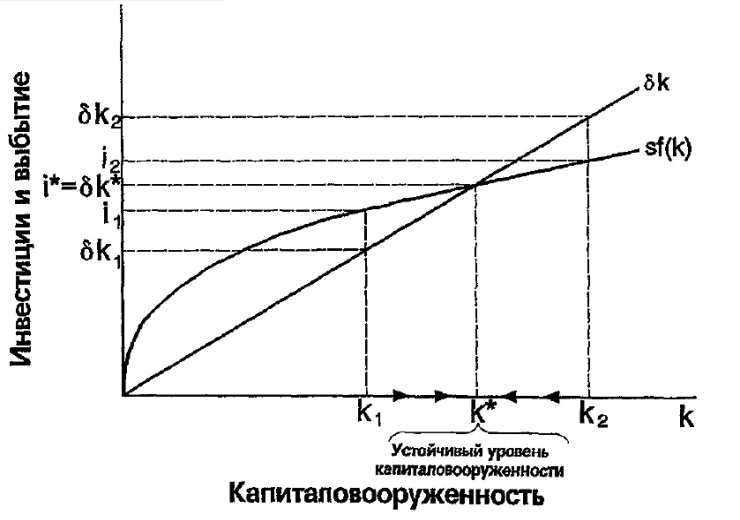 Влияние i и выбытия на запасы К можно выразить с помощью ур-я: ∆k = i – б* k, где ∆k изменение запасов К, приходящихся на 1 работника за год. Т.к. i = s, то ∆k = sf(k) – б* k.
Влияние i и выбытия на запасы К можно выразить с помощью ур-я: ∆k = i – б* k, где ∆k изменение запасов К, приходящихся на 1 работника за год. Т.к. i = s, то ∆k = sf(k) – б* k.


