Методика расчета
С учетом изложенного рассмотрим методику оценки суммарной погрешности при нормальном законе распределения ее составляющих
1. Пусть суммарная погрешность состоит из n составляющих
для каждой из которых заданы оценки среднего квадратического отклонения.
2. Эти составляющие погрешности подразделяют на аддитивные и мультипликативные
3.Из аддитивных погрешностей выделяют группы сильно коррелированных между собой составляющих погрешностей, и внутри этих групп производится алгебраическое суммирование оценок их среднего квадратического отклонения по формуле
где К- число коррелированных составляющих погрешности в данной i-группе;
4.После того как все группы аддитивных коррелированных погрешностей выделены и внутри их выполнено алгебраическое суммирование, суммарные погрешности для каждой из группам и оставшиеся вне групп остальные аддитивные погрешности можно считать уже некоррелированными и суммировать их по правилу геометрического суммирования.
Найденное таким путем среднее квадратическое отклонение аддитивной составляющей соответствует началу диапазона измерения.
5.Из мультипликативных погрешностей также выделяют группы сильно коррелированных между собой составляющих погрешностей, и внутри этих групп находят оценки их среднего квадратического отклонения.
6. После того, как для всех групп мультипликативных коррелированных погрешностей найдены их оценки, производится их геометрическое суммирование между собой и с остальными некоррелированными погрешностями, т.е. находят оценку среднего квадратического отклонения суммарной мультипликативной погрешности
7. Для определения оценки среднего квадратического отклонения погрешности в конце диапазона измерения геометрически суммируют результирующую аддитивную и мультипликативную составляющую:
8. Для заданной доверительной вероятности Р находят оценки доверительного интервала суммарной погрешности соответственно в начале и в конце диапазона измерения:
где t-коэффициент, значение которого в зависимости от принятой доверительной вероятности Р выбирают из таблицы.
9. Затем находят оценку суммарной погрешности для произвольного значения измеряемой величины в виде
где значения Таким образом, вероятностная оценка (2,2) учитывает как аддитивную, так и мультипликативную составляющую погрешности измерений.
|


 .
.
 означает, что для составляющих с положительной корреляцией нужно брать значение
означает, что для составляющих с положительной корреляцией нужно брать значение  со знаком (+), а для составляющих с отрицательной корреляцией - со знаком (-). Такое суммирование погрешностей называется алгебраическим суммированием. Абсолютные значения коэффициентов корреляции могут находится в пределах 0,7 -…1, поэтому алгебраическое суммирование обычно дает несколько завышенное значение суммарной погрешности.
со знаком (+), а для составляющих с отрицательной корреляцией - со знаком (-). Такое суммирование погрешностей называется алгебраическим суммированием. Абсолютные значения коэффициентов корреляции могут находится в пределах 0,7 -…1, поэтому алгебраическое суммирование обычно дает несколько завышенное значение суммарной погрешности.
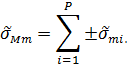




 (2.2)
(2.2) u
u  выражены в процентах.
выражены в процентах.


