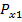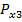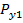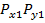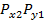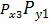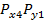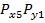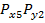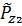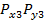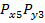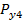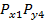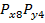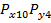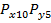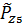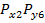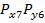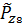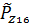Вероятностная оценка суммарной погрешности при заданных законах распределения каждой составляющей погрешности
Предложим, что суммарная погрешность
Очевидно, что эти формулы приводятся одна к другой заменой переменных. Использовав (1.1) можно рассчитать вероятность появления суммарной погрешности в заданный интервал ее измерения
При суммировании нескольких составляющих погрешности решение подобной задачи существенно осложняется, так как необходимо знать многомерный закон их распределения. Поэтому на практике обычно ограничиваются двумерной функцией распределения, поскольку в ряде случаев можно эту задачу можно решить по парным суммированием составляющих погрешности измерения. На практике часто приходится определять вероятностную оценку суммарной погрешности, состоящую и n – числа независимых случайных погрешностей Если для каждой составляющей погрешности заданы функции плотности вероятности
то можно найти функцию плотности вероятности суммарной погрешности следующим образом. Из теории вероятности известно, что если две случайные величины
а формулы для суммарного закона распределения этих двух погрешностей принимают вид интегральной операции свертки
Эти формулы обычно называют формулами композиции двух законов распределения, подразумевая под композицией нахождение закона распределения двух независимых случайных величин. Для обозначения композиции законов распределения часто применяют символическую запись
Пользоваться формулой (1.3) удобно тогда, когда законы распределения
Характеристическая функция суммы двух независимых погрешностей
а функция распределения суммарного закона путем обратного преобразования Фурье:
На практике вместо преобразования Фурье для отыскания Если число суммарных составляющих независимых погрешностей n, то суммирование и нахождение закона распределения суммарной погрешности производится последовательно, т.е. сначала находится композиция законов распределения первой и второй погрешностей, затем композиция законов распределения полученной и третьей погрешности, вновь полученной и четвертой и т.д.
После этого, используя найденный закон распределения суммарной погрешности (1.4) определяют вероятность появления суммарной погрешности в заданном интервале на основе выражения (1.2). При суммировании случайных погрешностей законы их распределения могут существенно деформироваться, т.е. форма закона распределения суммы может резко отличатся от формы распределения составляющих погрешности. Рассмотрим пример, когда суммарная погрешность состоит из двух составляющих, причем первая составляющая погрешности подчиняется нормальному закону распределения (рис. 1.1, кривая 1)
и вторая составляющая распределена равномерно в интервале (-а, а) (рис.1.1, кривая 2)
РИС.1.1 Используя (1.3) и учитывая, что
Делая подстановку
Если положить, что IаI=σ, то получим график, изображение на рис. 1.1 кривая 3 Некоторые примеры изменения формы закона распределения при образовании композиции показаны на рис 1,2.
Рис. 1,2.
Композиция двух равномерно распределенных погрешностей 9 рис 1.2.а) с шириной распределения b Рассмотрим примеры композиции различных законов распределений двух независимых случайных величин, для которых рассчитаны вероятности появления суммарной погрешности в заданном интервале по (1.2). Причем доверительный интервал ε;суммарной погрешности выражается через оценку среднего квадратического отклонения суммарной погрешности
где К – коэффициент, значение которого зависит от законов распределения суммируемых погрешностей и доверительной вероятности Р. На рис.1.3. показана зависимость К от доверительной вероятности Р (кривая 1), когда суммируются две погрешности с равномерными законами распределения, а также кривая 2 для нормального закона. Для большинства других симметричных законов распределения, таких как треугольного, трапецеидального, арксинусоидального, кривая К = f(Р) будет находится между кривыми 1 и 2. Следует иметь в виду что коэффициент К зависит не только от законов распределения суммируемых погрешностей, но и от соотношения их дисперсий. На рис.1.4, изображены зависимости коэффициента К для доверительной вероятности Р= 0,95 от относительного значения дисперсии
Рис 1.3 Рис 1.4
Нахождение композиции законов распределения по формуле (1.3) иногда связано с относительно громоздкими вычислениями, которых можно избежать, если воспользоваться численными методами выполнения интегральной операции свертки, хорошо разработанными в вычислительной математике. Эти численные методы можно также использовать, если законы распределения двух суммируемых составляющих погрешности найдены на основе экспериментальных данных и представлены в виде гистограмм. Рассмотрим, например, одну из методик численного приближенного метода, нахождения композиции законов распределения. Пусть известны плотности распределения Сначала следует разбить область измерения случайных величин х и у,в пределах которой плотности распределения существенно отличаются от нуля, на частичные интервалы равной ширины. Чем больше число частичных интервалов, тем точнее можно найти плотность распределения f(z) суммарной случайной величины (z).
а) б) РИС 1.5.
Первый и последний частичные интервалы могут выходить за границы возможных значений х и у. Затем рассчитывают вероятность нахождения случайных величин х и у соответственно для каждого частичного интервала
Если законы распределения случайных величин заданы в виде гистограмм, то вместо этих значений вероятности следует использовать соответствующие частоты. Результаты оформляются в виде таблицы 1.1. Таблица 1.1.
Затем необходимо найти композицию законов распределения, представляя приближенное выражение закона распределения суммарной случайной величины в виде таблицы, 1.2. Таблица 1.2.
Оценка вероятности
Оценка вероятности
Таблица 1.3.
Используя расчетные значения вероятностей В ряде случаев при суммировании случайных величин не наблюдается деформация законов распределения, Так пример, композиция нормальных распределений дает нормальное распределение, композиция пуассоновских распределений дает пуассоновское распределение, композиция биноминальных распределений приводив снова к биноминальному распределению.
|

 состоит из двух случайных составляющих
состоит из двух случайных составляющих  , и задана совместная функция распределения этих величин
, и задана совместная функция распределения этих величин 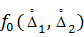 . Тогда плотность распределения суммы этих двух случайных погрешностей определяется выражением
. Тогда плотность распределения суммы этих двух случайных погрешностей определяется выражением
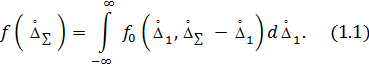



 и
и  независимы, то двумерная плотность вероятности
независимы, то двумерная плотность вероятности 



 заданы одной формулой во всем диапазоне значений аргументов (от -
заданы одной формулой во всем диапазоне значений аргументов (от -  ). В противном случае удобнее произвести композицию двух законов распределения, используя характеристические функции. Известно, что характеристическую функцию случайной величины
). В противном случае удобнее произвести композицию двух законов распределения, используя характеристические функции. Известно, что характеристическую функцию случайной величины  можно найти как преобразование Фурье от закона распределения
можно найти как преобразование Фурье от закона распределения  , если в преобразовании изменить знак „минус” на „плюс” перед w
, если в преобразовании изменить знак „минус” на „плюс” перед w
 определяется как произведение характеристических функций этих погрешностей
определяется как произведение характеристических функций этих погрешностей ,
,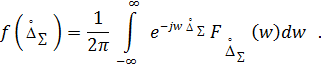
 и
и  можно также пользоваться таблицами прямого и обратного одностороннего преобразования Лапласа, сдвигая функцию распределения
можно также пользоваться таблицами прямого и обратного одностороннего преобразования Лапласа, сдвигая функцию распределения 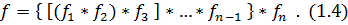
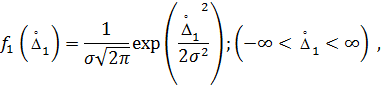

 в интервале (-а, а), находим плотность композиции двух законов распределения
в интервале (-а, а), находим плотность композиции двух законов распределения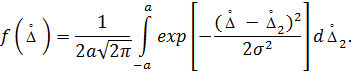
 , получаем
, получаем
 a дает распределение суммарной погрешности в виде трапеции с верхним основанием a-b и нижним a+b. Композиция двух одинаковых равномерных распределений приводит к треугольному закону распределения (рис.1.2, б), (распределение Симпсона). Так как в этом случае верхнее основание трапеции обращается в нуль, а нижнее – в 2а. Композиция равномерного распределения и распределения Лапласа приводит к закону распределения суммарной погрешности, показанной на (рис.12, в). Композиция нормального и двухзначного дискретного распределения дает кругло вершинное двух модальное распределения суммарной погрешности. Композиция экспоненциального и равномерного распределений приводит к так называемому распределению класса Шапо. Композиция распределения Лапласа и дискретного двухзначного распределения приводит к островершинному двух модальному распределению суммарной погрешности.
a дает распределение суммарной погрешности в виде трапеции с верхним основанием a-b и нижним a+b. Композиция двух одинаковых равномерных распределений приводит к треугольному закону распределения (рис.1.2, б), (распределение Симпсона). Так как в этом случае верхнее основание трапеции обращается в нуль, а нижнее – в 2а. Композиция равномерного распределения и распределения Лапласа приводит к закону распределения суммарной погрешности, показанной на (рис.12, в). Композиция нормального и двухзначного дискретного распределения дает кругло вершинное двух модальное распределения суммарной погрешности. Композиция экспоненциального и равномерного распределений приводит к так называемому распределению класса Шапо. Композиция распределения Лапласа и дискретного двухзначного распределения приводит к островершинному двух модальному распределению суммарной погрешности.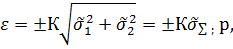
 второй составляющей погрешности в суммарной погрешности, т.е. от
второй составляющей погрешности в суммарной погрешности, т.е. от  . Кривая 1 соответствует композиции двух арксинусоидальных распределений погрешности, кривая 2- композиции арксинусоидального распределения погрешности с
. Кривая 1 соответствует композиции двух арксинусоидальных распределений погрешности, кривая 2- композиции арксинусоидального распределения погрешности с  и равномерного распределения погрешности с
и равномерного распределения погрешности с 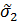 ,кривая 3 - композиции двух равномерного распределенных погрешностей, кривая 4 – композиции равномерно распределенной погрешности с нормально распределенной, кривая 5 – композиции двух нормально распределенных погрешностей. Анализ зависимостей К = f(Р) показывает, что только при композиции нормальных распределений коэффициент К не зависит от отношения дисперсий суммируемых погрешностей.
,кривая 3 - композиции двух равномерного распределенных погрешностей, кривая 4 – композиции равномерно распределенной погрешности с нормально распределенной, кривая 5 – композиции двух нормально распределенных погрешностей. Анализ зависимостей К = f(Р) показывает, что только при композиции нормальных распределений коэффициент К не зависит от отношения дисперсий суммируемых погрешностей. суммируемых случайных величин z = x + y (рис.1.5, а, б).
суммируемых случайных величин z = x + y (рис.1.5, а, б).
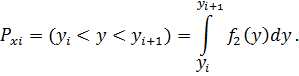


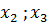





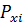


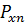







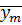



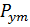








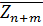

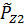


 -середина частичного интервала
-середина частичного интервала  , ширина которого равна ширине интервалов
, ширина которого равна ширине интервалов  , u
, u  т.е.
т.е.  ,K=2,3,…..,n+m.
,K=2,3,…..,n+m.
 , из которой видно, что произведения вероятностей, подлежащих суммированию по формуле (1.5), расположены вдоль диагоналей, нанесенных штриховыми линиями.
, из которой видно, что произведения вероятностей, подлежащих суммированию по формуле (1.5), расположены вдоль диагоналей, нанесенных штриховыми линиями.