Приближенные способы оценки суммарной погрешности без установления закона ее распределения
При вероятностно - статистической оценке суммарной погрешности проектируемого средства измерений, как правило, известны только границы составляющих погрешностей. Обычно считают, что эти составляющие погрешности с равной вероятностью могут иметь любые значения в пределах указанных границ На чем основывается такое допущение? Прежде всего на том, что для случайной величины, изменяющейся в заданных границах, из возможных симметричных аппроксимаций плотности распределения: нормального, равномерного, треугольного и трапециевидного, именному равномерному распределению соответствует максимальная энтропия. Поэтому такое допущение дает оценку сверху среднего квадратического отклонения, и на практике приводит к реалистическим оценка погрешностей. Известно, что дисперсия равномерного распределения определяется по формуле.
Можно также показать, что сумма большого числа случайных независимых величин, подчиняющихся равномерному закону распределения вероятности, подчиняется нормальному закону. Поэтому доверительный интервал суммарной систематической погрешности, состоящей из m составляющих (m→
А при доверительной вероятности Р=0,99 - не будет выходить за пределы доверительного интервала
В общем случае доверительный интервал суммарной погрешности находят по формуле
где Значения коэффициента Таблица 3.1
При Р=0,99 коэффициент Таблица 3.2
Параметр
|

 т.е. принимаются равномерный закон их распределения.
т.е. принимаются равномерный закон их распределения.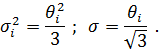
 ),с доверительной вероятностью Р=0,95 не будет выходить за пределы доверительного интервала
),с доверительной вероятностью Р=0,95 не будет выходить за пределы доверительного интервала 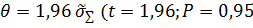 для нормального закона)
для нормального закона)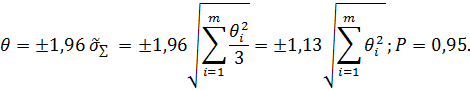
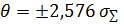 (t=2,576;P=0,99 для нормального закона)
(t=2,576;P=0,99 для нормального закона)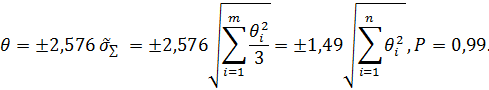
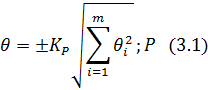
 – коэффициент, зависящий от доверительной вероятности Р, числа составляющих m и от соотношения между составляющими.
– коэффициент, зависящий от доверительной вероятности Р, числа составляющих m и от соотношения между составляющими. (ГОСТ 8.207-76) рекомендуется принимать среднее значение
(ГОСТ 8.207-76) рекомендуется принимать среднее значение 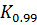 =1,4, а при m
=1,4, а при m  4 значение
4 значение 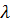
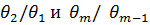 где
где 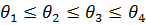 .
.


