Методика расчета. Рассмотрим методику оценки суммарной погрешности для случая, когда систематические составляющие погрешности заданы границами ее изменения и предполагается
Рассмотрим методику оценки суммарной погрешности для случая, когда систематические составляющие погрешности заданы границами ее изменения
1. Все систематические и случайные составляющие погрешности подразделяют на аддитивные и мультипликативные. 2. Для аддитивных систематических составляющих погрешностей оценивают доверительный интервал суммарной аддитивной погрешности используя (3.1) для выбранной доверительной вероятности Р:
3. Из аддитивных случайных составляющих погрешностей выделяют группы сильно коррелированных между собой погрешностей и внутри этих групп проводят алгебраическое суммирование оценок их среднего квадратического отклонения
4. После того, как все группы аддитивных коррелированных случайных погрешностей выделены и внутри их выполнено суммирование, суммарные по группам и оставшиеся вне группы остальные аддитивные случайные погрешности суммируют по правилу геометрического суммирования:
5. Затем рассчитывают оценку доверительного интервала суммарной погрешности в начале диапазона измерения с учетом как систематической, так и случайной погрешности, используя эмпирическую формулу, рекомендованную ГОСТ8.207 - 76:
где
6. Доверительный интервал суммарной систематической погрешности оценивают с учетом как аддитивных, так и мультипликативных составляющих по (3.1)
7. Затем для мультипликативных случайных составляющих оценивают среднее квадратическое отклонение суммарной погрешности по методике, изложенной в n. 3 и n 4 и находят 8. Далее рассчитывают оценку доверительного интервала суммарной погрешности с учетом всех составляющих в конце диапазона измерения:
9 Представляют оценку суммарной погрешности для произвольного значения измеряемой величины в виде
где Рассмотрим приближенные способы определения доверительного интервала суммарной погрешности, если для каждой составляющей погрешности задается среднее квадратическое отклонение без установления закона их распределения. В этом случае методикa оценки суммарной погрешности до момента расчета оценок среднего квадратического отклонения суммарной погрешности соответственно в начале и в конце диапазона измерения В этом случае можно использовать два подхода. Известно, что для большой группы классов различных распределений доверительный интервал
соответствует доверительности вероятности Р=0,9 с погрешностью
Поэтому можно считать, что при суммировании погрешностей любого сочетания распределений из этой группы классов распределение суммарной погрешности также будет принадлежать этой группе классов. Тогда для доверительной вероятности Р=0.9 можно будет определить оценки доверительного интервала суммарной погрешности в начале и в конце диапазона измерения
и далее представить оценку суммарной погрешности для Р=0,9 в виде (3.1). Можно использовать другой поход упрощенной методики оценки суммарной погрешности. Она основывается на центральной предельной теореме теории вероятности. При суммировании большого числа независимых составляющих погрешностей с соизмеримыми дисперсиями закон распределения суммарной погрешности все более приближается к нормальному, особенно в области больших значений плотности вероятности. В этом случае можно полностью использовать методику расчета приведенную ранее, однако оценку суммарной погрешности предпочтительнее представлять с доверительной вероятностью не более 0,95. Тем не менее использовать этот метод следует при невысоких требованиях к точности получаемого результата, поскольку при конечном числе суммируемых погрешностей реальное распределение может заметно отличаться от нормального. Так, например, чтобы получить нормальное распределение суммарной погрешности при суммировании арккосинусных распределений, нужно иметь по крайней мере более десяти слагаемых.
4. Варианты контрольных заданий по расчету суммарной погрешности
Контрольная работа 1
Приведите методику расчета вероятностной оценки суммарной погрешности, если каждая случайная составляющая имеет нормальное распределение и заданы СКО. (таб. 4.1) Численный результат измерения представить с доверительной вероятностью Р=0,95, если цифрой вольтметр на пределе измерения 100В показывает Ux=85.23В. Решить задачу для своего варианта.
Контрольная робота 2
Приведите методику расчета вероятностной оценки суммарной погрешности с учетом как систематических составляющих, так и случайных составляющих, когда каждая систематическая составляющая погрешности задана интервалом ее изменения Численный результата измерения представить с доверительной вероятностью Р=0.95, если цифровой вольтметр на пределе измерения 100В показывает Uк= 89.25В.
Таблица 4,1
Талица 4,2
5 Пример расчёт вероятностной оценки суммарной случайной погрешности Приведем методику расчёта вероятностной оценки суммарной случайной погрешности, если каждая случайная составляющая имеет нормальное распределение и заданы СКО. Численный результат измерения представляем с доверительной вероятностью Р=0,95, если некий цифровой прибор, имеющий максимальный диапазон измерения XК=100В (физических единиц), показывает значение: Х=30+(а+b) (физических единиц), где (а+b) – сумма двух последних цифр зачетки. Номер зачетки №209016 Х=30+(1+6)=30+7=37 Исходные данные берутся из таблицы 5.1 и таблицы 5.2:
Таблица 5.1.СКО для случайных составляющих погрешностей
Таблица 5.2.Коэфициенты корреляционной связи
Задание. Приведите расчёт вероятностной оценки суммарной случайной погрешности, если каждая случайная составляющая погрешности имеет нормальное распределение и заданы СКО. Численный результат измерения представить с доверительной вероятностью Р = 0,95; если:
1.Суммарная погрешность состоит из 9-ти составляющих
2.Все составляющие погрешности делим на две группы: 1-я аддитивная; 2-я мультипликативная. 1-я:
3. Из первой группы аддитивных погрешностей выбираем сильно коррелированные между собой составляющие погрешности и внутри этих групп произведем алгебраическое суммирование оценок их СКО,т.е.:
1-вая группа сильно коррелированных погрешностей.
4. Определяем оценку СКО суммарной аддитивной погрешности, (некоррелированных) и суммировать можно по правилу геометрического суммирования:
5. Находим доверительный интервал случайной составляющей погрешности в начале диапазона измерения для доверительной вероятности: Р=095, т.е. γH=±t* γH=±2*0.32= 6. Для сильно коррелированных мультипликативных погрешностей в пределах каждой из групп произведем алгебраическое суммирование СКО:
7. Определяем оценку СКО суммарной мультипликативной погрешности, используя правило геометрического суммирования:
8.Находим СКО суммарной погрешности в конце диапазона измерений путем геометрического суммирования аддитивной и мультипликативной составляющих:
9. Определяем доверительный интервал случайной составляющей погрешности в конце диапазона измерения c доверительной вероятностью: γK=±t* γK=±2*0.58=±1.16%,Р=0.95 10.Представляем вероятностную оценку суммарной погрешности для заданного значения измеряемой величины Х:
γ(37)=±{1.16+0.64*( 11. запишите результат измерения с указанием оценки доверительного интервала погрешности, выраженной в единицах измеряемой величины
(x ∆= Ответ: (37,0±1,1)В, Р=0,95. Выполняем округление погрешности и записываем результат измерения: X=(37,0±1.11)В,Р=0,95. Результат измерения находится в диапазоне от 35,9 В до 38.1В с доверительной вероятностью Р=0.95
|

 и предполагается, что они имеют равномерное распределение, а для случайных составляющих погрешности известны оценки их среднего квадратического отклонения
и предполагается, что они имеют равномерное распределение, а для случайных составляющих погрешности известны оценки их среднего квадратического отклонения  и считается, что они имеют нормальное распределение.
и считается, что они имеют нормальное распределение.



 - коэффициент, зависящий от соотношения случайной и систематической составляющих погрешности, который рассчитывается при значениях коэффициентов
- коэффициент, зависящий от соотношения случайной и систематической составляющих погрешности, который рассчитывается при значениях коэффициентов  u t, соответствующих одному и тому же значению доверительной вероятности Р:
u t, соответствующих одному и тому же значению доверительной вероятности Р:
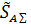 - оценка суммарного среднего квадратического отклонения суммарной аддитивной погрешности:
- оценка суммарного среднего квадратического отклонения суммарной аддитивной погрешности:




 - оценка среднего квадратического отклонения суммарной погрешности в конце диапазона измерения:
- оценка среднего квадратического отклонения суммарной погрешности в конце диапазона измерения:

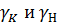 выражены в процентах и определены соответственно в n.5 и n.8 для одного и того же значения доверительной вероятности.
выражены в процентах и определены соответственно в n.5 и n.8 для одного и того же значения доверительной вероятности. и
и  ничем не отличается от методики, приведенной ранее. Наиболее трудным является определение интервальной оценки суммарной погрешности в начале и в конце диапазона измерения, так как для этого необходимо знать закон распределения суммарных погрешностей.
ничем не отличается от методики, приведенной ранее. Наиболее трудным является определение интервальной оценки суммарной погрешности в начале и в конце диапазона измерения, так как для этого необходимо знать закон распределения суммарных погрешностей.


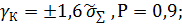
 , а для случайных составляющих, имеющих нормальное распределение, заданы СКО=
, а для случайных составляющих, имеющих нормальное распределение, заданы СКО= 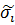 (таб. 4.2)
(таб. 4.2)



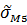

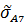
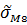


 =-1
=-1
 =1
=1
 =-1
=-1


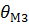




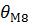
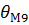

 0,2
%
0,2
%
 A1,%
A1,%
 A1 =0,15% XН=100 В
A1 =0,15% XН=100 В

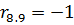

 ;
; 2-я:
2-я: 

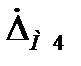





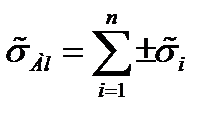
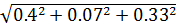 = 0.32%
= 0.32%
 =0.27%
=0.27%
 =0.58%
=0.58% ,где
,где  = 100 В;
= 100 В;  = 37 В
= 37 В -1)}=±3,064%,Р=0.95
-1)}=±3,064%,Р=0.95
 (x)), Р = 0,95.
(x)), Р = 0,95. =
=  =1.11 В
=1.11 В


