Определители квадратных матриц
Каждой квадратной матрице А можно поставить в соответствие число, которое называется её определителем и обозначается det A, ∆ или |A|. · Определитель матрицы 2-ого порядка (2) вычисляется по формуле: det A = Схема вычисления:
Пример 9 Вычислить определитель матрицы А= Решение:
Схема вычисления по правилу треугольника:
Схема вычисления по правилу Саррюса:
_ + _ + _ +
- к исходному определителю приписывают два первых столбца и составляют две группы произведений. Пример 10 Вычислить определитель матрицы
а) вычислим определитель по правилу треугольника, используя рис.4:
б) вычислим определитель оп правилу Саррюса, используя рис.5:
― +
Пример 11 Вычислить определитель Решение:
(по правилу треугольника)
Пример 12. Вычислить алгебраическое дополнение элементов
Решение:
Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
В частности,
Пример 13. Вычислить определитель из примера 10 путем его разложения по элементам 1-ой строки; 2-ой строки. Решение а) ∆=
б) ∆=
Замечание 5: При выборе знака перед минором в алгебраическом дополнении нужно руководствоваться следующим правилом:
1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером (транспонирование определителя). Например,
2. Перестановка двух строк (или столбцов) определителя равносильна его умножению на (-1). Например,
3. Умножение всех элементов одной строки (или одного столбца) определителя на
4. Определитель равен нулю, если: все элементы
(строки пропорциональны: вторая строка получается путем умножения всех элементов первой на 2) 5. Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), предварительно умноженные на
Пример 14 Вычислить определитель 4-ого порядка: Решение: Используем теорему разложения и свойства определителей. Прибавим ко второй строке первую, умноженную на (-2), к третьей – первую, умноженную на (-1), к четвертой – первую. После этого все элементы первого столбца, кроме первого элемента, будут равны нулю. Применяя теорему разложения к этому столбцу, понизим порядок определителя:
Полученный определитель 3-его порядка можно вычислить по правилу треугольника (рис.4), по правилу Саррюса (рис.5). Удобно применить теорему разложения ко второй строке:
Пример 15 Вычислить определитель
Решение: · Поменяем местами первую и четвертую строки:
· Прибавим ко второй строке первую, умноженную на (-7), к четвертой первую, умноженную на (-2).
· применили теорему разложения к первому столбцу, далее, общий множитель у элементов третьей строки 3 вынесем за знак определителя и для вычисления последнего применили правило треугольника.
|

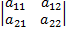 =
= 
 рис.3
рис.3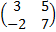

 =
= 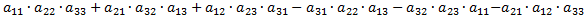
 рис.4
рис.4 рис.5
рис.5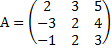

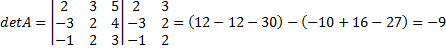
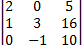 .
. ∙
∙ 
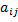 определителя называется определитель, который получается из данного путем вычеркивания i-ой строки и j-ого столбца, на пересечении которых стоит элемент
определителя называется определитель, который получается из данного путем вычеркивания i-ой строки и j-ого столбца, на пересечении которых стоит элемент  .
.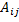 элемента
элемента 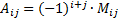
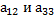 определителя
определителя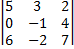
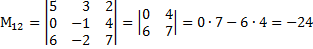
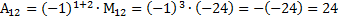
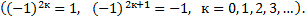


 , j= 1, 2, …, n.
, j= 1, 2, …, n.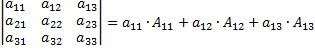 – вычисление определителя путем разложения по элементам 1-ой строки.
– вычисление определителя путем разложения по элементам 1-ой строки.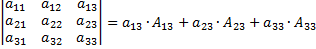 – вычисление определителя путем разложения по элементам 3-его столбца.
– вычисление определителя путем разложения по элементам 3-его столбца.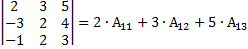 (по элементам 1-ой строки)
(по элементам 1-ой строки)
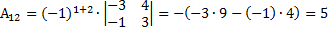

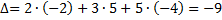
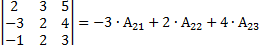 (по элементам 2-ой строки)
(по элементам 2-ой строки)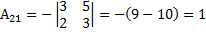

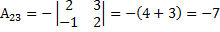
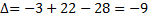
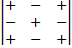
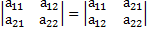

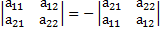
 ;
;  ;
;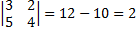 .
.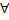 (
(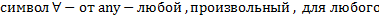 ) число К равносильно умножению определителя на это число К. Например,
) число К равносильно умножению определителя на это число К. Например,



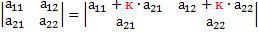
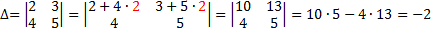
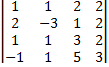
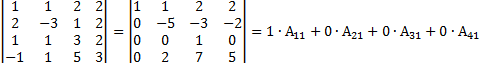 =
=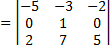
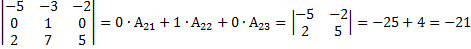
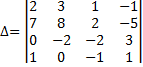

 =
=



