Системы линейных алгебраических уравнений (СЛАУ)
Уравнение вида:
где a1, a2, an, b - некоторые постоянные, называется линейным уравнением с n неизвестными x1, x2, …, xn. В курсе средней школы рассматривали линейные уравнения с одним, двумя, тремя неизвестными; это уравнения: a · x = b; a · x + by = с; ax + by + с · z = d. C геометрической точки зрения, эти уравнения изображают соответственно точку на числовой прямой, прямую на плоскости, плоскость в пространстве. · Системой линейных алгебраических уравнений называют два либо больше уравнений, которые решаются совместно. Это означает, что решением системы будут те решения её уравнений, которые удовлетворяют всем уравнениям системы. В частности, система двух линейных уравнений с двумя неизвестными x, y имеет вид:
Система трех линейных уравнений с тремя неизвестными x, y, z имеет вид:
В общем случает система m линейных алгебраических уравнений с n неизвестными записывается в виде:
где через аij обозначен коэффициент при неизвестном xj в i-ом уравнении системы (i = 1, 2, …, m; j = 1, 2, …, n), x1, x2, …, xn - неизвестные, а числа b1, b2, …, bm - называются свободными членами.
В матричной форме система (7) имеет вид: A · X = B, (8) где А = X = B = · Решением системы (7) называется n значений неизвестных · Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. · Совместная система называется определённой, если она имеет единственное решение и неопределённой, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы.
· Совокупность всех частных решений называется общим решение системы. · Две системы называются эквивалентными (равносильными),если они имеют одинаковые решения или обе несовместны. Пример 18 Решить систему уравнений
Решение: Имеем систему линейных алгебраических уравнений с двумя неизвестными Из «школьной» алгебры знаем методы:
а) Метод подстановки. Из 2-ого уравнения
подставим найденное выражение в 1-ое уравнение, в результате получится одно уравнение с одним неизвестным: 2 (13 + 2 2 LnhtbEyPwW7CMBBE75X4B2uReis2tKYljYMAqeq50As3J94mUeN1iA2kf9/tqdx2NKOZt/l69J24 4BDbQAbmMwUCqQqupdrA5+Ht4QVETJac7QKhgR+MsC4md7nNXLjSB172qRZcQjGzBpqU+kzKWDXo bZyFHom9rzB4m1gOtXSDvXK57+RCqaX0tiVeaGyPuwar7/3ZGzi8ezWWqd0hnZ7V5rjVSzpqY+6n 4+YVRMIx/YfhD5/RoWCmMpzJRdEZ0HPN6MnAagGCff2kVyBKPh4VyCKXtw8UvwAAAP//AwBQSwEC LQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQBhXkkm8QEAAOkDAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJv RG9jLnhtbFBLAQItABQABgAIAAAAIQBwVEgD3AAAAAgBAAAPAAAAAAAAAAAAAAAAAEsEAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAVAUAAAAA " strokecolor="black [3200]" strokeweight=".5pt">
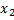 + 3 + 3 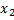 = 12 = 12
7
тогда: Ответ:
б) Метод сложения. Умножим левую и правую части 2-ого уравнения на (-2):

Сложим почленно уравнения системы: 7 Подставим найденное значение в любое из уравнений исходной системы, пусть во 2-ое: Ответ: x1 = 9, x2 = -2.
Замечание 7: Коэффициенты при неизвестных уравнениях системы (5) не пропорциональны => система определённая.
Пример 19 Решить систему уравнений
Решение: Система неопределённая. Действительно, если обе части второго уравнения разделить на (-2), то получится первое уравнение, и система двух уравнений сводится к одному уравнения с двумя неизвестными, а именно: x1 – 2х2 = 13.
Система имеет бесчисленное множество решений, задаваемых формулой: x1 = 13 + 2х2. Задавая произвольные значения неизвестному x2, получаем соответствующие значения x1. Пусть, например x2 = 0, тогда x1 = 13. При x2 = 1 = Замечание 8: Если коэффициенты при неизвестных и свободные члены в уравнениях системы (5) пропорциональны, следовательно, система неопределённая,решениями является любая пара (х,у), удовлетворяющая любому уравнению системы.
Пример 20 Решить систему уравнений
Решение: Система несовместна, т.к. одно выражение системы не может одновременно равняться различным значениям. Ответ: решения нет. Замечание 9: Если коэффициенты при неизвестных в уравнениях системы (5) пропорциональны, но они не пропорциональны свободным членам, то система несовместна. Пример 21 Системы х1 = 9, х2 = -2. Основными методами решения СЛАУ являются метод Крамера, матричный метод и метод Гаусса. Первые два метода применимы только для решения систем с квадратной невырожденной матрицей. Методом Гаусса можно решать любые СЛАУ.
|

 ·
· 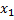 +
+ 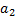 ·
·  ·
·  = b,
= b,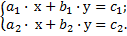 (5)
(5) (6)
(6) (7),
(7), - матрица системы (порядок m x n), (9)
- матрица системы (порядок m x n), (9)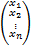 - матрица – столбец неизвестных (порядок n x 1),
- матрица – столбец неизвестных (порядок n x 1), - матрица - столбец свободных членов (порядок m x 1).
- матрица - столбец свободных членов (порядок m x 1). , …,
, …,  , при подстановке которых в (7) все уравнения системы обращаются в верные равенства.
, при подстановке которых в (7) все уравнения системы обращаются в верные равенства. = 13 + 2
= 13 + 2 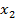 ,
,
 = b
= b
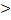

 - система,эквивалентная данной
- система,эквивалентная данной


 эквивалентны,
эквивалентны, 


