Действия над матрицами
1) Матрицы А и В одной размерности считаются равными, если равны их соответствующие элементы:А=В ó 2) Сложение(вычитание) матриц одинакового размера осуществляется поэлементно: С = А + В, если 3) Умножение матрицы на число λ; – каждый элемент матрицы умножается на это число: B = λ × A, если 2) и 3) - линейные операции над матрицами.
Замечание 1: Сложение (вычитание) и умножение матрицы на число – линейные операции над матрицами. Пример 2 Найти сумму матриц A + B из Примера 1 Решение: А + В = Замечание 2: Матрица А + Всимметричная, справедливо равенство: А + В = Пример 3 Найти линейную комбинацию матриц 2А + А = Решение: 2 ∙ А = 2А + 4) Умножение матриц. Произведение А ∙ В определяется не для произвольных матриц А и В. Оно имеет смысл только в том случае, когда число столбцов матрицы А ровно числу строк В. При этом А ∙ В есть матрица С, каждый элемент
Найти произведения матриц: Пример 4
Пример 5
Пример 6 А ∙ В=
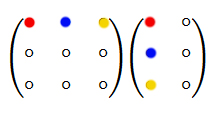
А ∙ В = На рисунке 1 схематично показано получение элемента
Рисунок 1
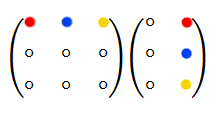
Рисунок 2 получение элемента
Рисунок 2
Пример 7 B ∙ A=
Замечание 3: В общем случае АВ ≠ ВА (примеры 6-7). 5) Матрицы, для которых выполняется равенство АВ = ВАназываются коммутативными. Пример 8 А ∙ В = А ∙ В = 0 (Хотя А ≠ 0, В ≠ 0) Замечание 4: В теории матриц нулевая матрица 0 и единичная Е играют роль чисел соответственно 0 и 1 в арифметике, т.е. ЕА = АЕ = А, А ∙ 0 = 0 ∙ А = 0, А + 0 = 0 + А.
|

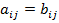
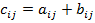
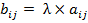
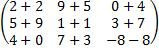 =
= 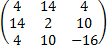
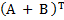 .
.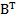 - 4Е, если
- 4Е, если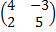 , В =
, В = 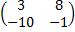 , Е =
, Е = 
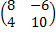 ,
, 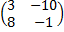 , 4Е =
, 4Е = 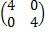 .
.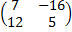
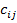 которой равен сумме последовательных произведений элементов i- той строки матрицы А на соответствующие элементы j - тогостолбца матрицы В.
которой равен сумме последовательных произведений элементов i- той строки матрицы А на соответствующие элементы j - тогостолбца матрицы В.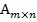 ∙;
∙; 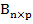 =
=  ó;
ó;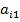 ∙;
∙; 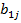 +
+ 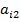 ∙;
∙; 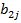 + … +
+ … + 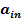 ∙;
∙; 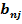 =
= 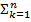
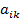 ∙
∙ 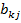 ,i =
,i =  , j =
, j = 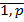 .
. 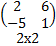 ∙
∙ 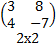 =
= 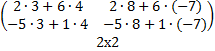 =
= 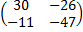
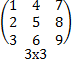 ∙
∙ 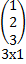 =
= 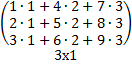 =
= 
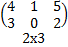 ∙
∙ 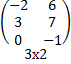 =
= 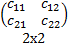
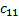 = 4 ∙ (-2) + 1 ∙ 3 + 5 ∙ 0 = -5
= 4 ∙ (-2) + 1 ∙ 3 + 5 ∙ 0 = -5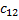 = 4 ∙ 6 + 1 ∙ 7 + 5 ∙ (-1) = 26
= 4 ∙ 6 + 1 ∙ 7 + 5 ∙ (-1) = 26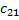 = 3 ∙ (-2) + 0 ∙ 3 + 2 ∙ 0 = -6
= 3 ∙ (-2) + 0 ∙ 3 + 2 ∙ 0 = -6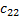 = 3 ∙ 6 + 0 ∙ 7 + 2 ∙ (-1) = 16
= 3 ∙ 6 + 0 ∙ 7 + 2 ∙ (-1) = 16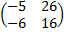
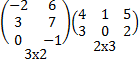 =
= 
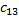 = -2 ∙ 5 + 6 ∙ 2 = 2;
= -2 ∙ 5 + 6 ∙ 2 = 2;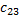 = 3 ∙ 5 + 7 ∙ 2 = 29;
= 3 ∙ 5 + 7 ∙ 2 = 29;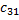 = 0 ∙ 4 + (-1) ∙ 3 = -3;
= 0 ∙ 4 + (-1) ∙ 3 = -3; 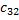 = 0 ∙ 1 + (-1) ∙ 0 = 0;
= 0 ∙ 1 + (-1) ∙ 0 = 0; 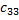 = 0 ∙ 5 + (-1) ∙ 2 = -2.
= 0 ∙ 5 + (-1) ∙ 2 = -2.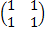 ∙;
∙; 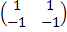 =
= 



