Решение СЛАУ по формулам Крамера
Пусть имеется система (6):
Определитель
Если элементы первого столбца этого определителя заменить на числа
При замене второго столбца определителя
Аналогично получаем определитель
·
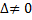 , то система (6) имеет единственное решение, которое определяется по формулам Крамера: , то система (6) имеет единственное решение, которое определяется по формулам Крамера:
(10)
· Если · Если Пример 22: Решить систему уравнений, используя формулы Крамера (10).
Решение: Определитель системы равен
Вычислим вспомогательные определители:
Решение системы:
Ответ:
Решение СЛАУ матричным методом
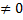 . Умножив обе части матричного уравнения (8) A · X = B слева на матрицу . Умножив обе части матричного уравнения (8) A · X = B слева на матрицу 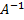 , получим: , получим:
Е · Х = Х = Пример 23 Решить систему уравнений матричным методом.
Решение: А= Найдем все алгебраические дополнения матрицы А:
Получим решение системы, используя формулу (11): Х = Ответ:
|

 ,
,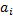 ,
, 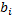 ,
, 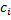 и
и 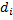 (i
(i 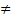
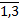 ) - заданные числа, х, y, z – неизвестные.
) - заданные числа, х, y, z – неизвестные. этой системы равен:
этой системы равен: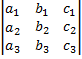 .
.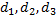 , то получим определитель
, то получим определитель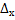 =
= 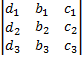 .
.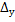 =
=  .
.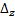 =
=  .
.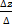
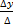
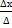
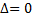 и хотя бы один из определителей,
и хотя бы один из определителей, 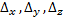 не равен нулю, то система несовместна.
не равен нулю, то система несовместна.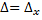 =
= 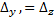 = 0, то система несовместна или имеет бесконечно много решений.
= 0, то система несовместна или имеет бесконечно много решений.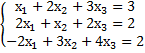
 = 4+18-8+6-6-16 = -2
= 4+18-8+6-6-16 = -2 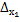 =
=  = 12+18+8-6-18-16 = -2
= 12+18+8-6-18-16 = -2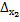 =
=  = 2 · 2 ∙
= 2 · 2 ∙  = 4 · (2+3-3+3-1-6) = -8
= 4 · (2+3-3+3-1-6) = -8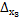 =
=  = 2+18-8+6-6-8 = 4
= 2+18-8+6-6-8 = 4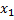 =
= 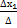 =
= 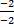 = 1
= 1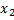 =
= 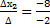 = 4
= 4 =
= 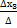 =
= 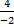 = -2
= -2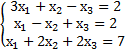
 – матрица системы, В =
– матрица системы, В = 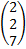 – столбец свободных членов, Х =
– столбец свободных членов, Х = 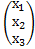 – столбец неизвестных.
– столбец неизвестных.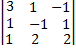 = -6-2+1-1-6-2 = -16
= -6-2+1-1-6-2 = -16 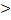 Ǝ
Ǝ 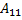 = -4
= -4
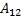 = -1
= -1
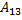 = 3
= 3
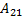 = -4
= -4
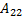 = 7
= 7
 = -5
= -5
 = 0
= 0
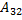 = -4
= -4
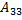 = -4
= -4
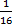
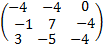
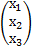 = -
= -  = -
= -  =
=