Задания для подготовки к зачету
I вариант 1. Вычислить 2А-В, если
2. Найти произведение матриц, если
3. Решить систему линейных уравнений методом Крамера: 4. Вычислить предел функции
5. Найти производную функции 6. Найти дифференциал функции в точке: у= 7. Найти интеграл а)
8. Сколькими способами можно составить 5 видов комплектов посуды из 26 возможных?
II вариант 1. Вычислить: 3А+2В, если
8. Сколькими способами можно составить 4 вида комплектов мебели из 19 возможных?
III вариант 1. Вычислить 4А-2В, если А=
2. Найти произведение матриц, если: А=
3. Решить систему линейных уравнений методом Крамера:
4. Вычислить предел функции: a) 5. Найти производную функцию: У= 6. Найти дифференциал функции в точке: у= 7. Найти интеграл: а)
8. Сколькими способами можно составить 4 вида комплектов фреже из 23 возможных?
IV вариант 1. Вычислить 5А-3В, если: А=
2. Найти произведение матриц В А=
3. Решить систему линейных уравнений методом Крамера:
4. Вычислить предел функции: а) 5. Найти производную функции: У= 6. Найти дифференциал функции в точке: У= 7. Найти интеграл: а)
8. Сколькими способами можно укомплектовать 6 гостиничных номеров из 36 возможных? V вариант 1. Вычислить 6А-4В+Е, если: А=
2. Найти произведение матриц В А=
3. Решить систему линейных уравнений методом Крамера:
4. Вычислить предел функции: а)
5. Найти производную функции: У= 6. Найти дифференциал функции в точке: У= 7. Найти интеграл: а) 8. Сколькими способами можно выбрать 4 комплекта посуды из 32 возможных?
Вопросы для подготовки к зачету 1. Что такое матрица, виды матрицы. 2. Линейные операции над матрицами. 3. Правила умножения матриц. 4. Формулы и метод Крамера решение систем линейных уравнений. 5. Определение предела функции. 6. Формулы первого и второго замечательных пределов. 7. Определение производной, ее геометрический и физический смысл. 8. Вычисление производной сложной функции. 9. Дифференциал, ее геометрический и физический смысл. 10. Неопределенный интеграл, его вычисление. 11. Методы интегрирования (прямое, подстановки). 12. Определенный интеграл. Формула Ньютона-Лейбница. 13. Определение комплексного числа, действие над комплексными числами. 14. Понятие факториала, перестановки, размещения, сочетания. 15. Определение и вычисление вероятности события.
|

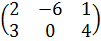 , В=
, В= 








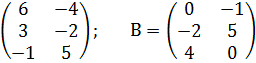



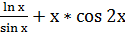

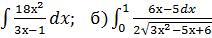
 , В=
, В= 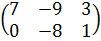


 ; б)
; б)  ; в)
; в) 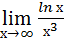 ;
;

 при х=
при х= 


 dx; б)
dx; б) 
 , В=
, В= 
 , если
, если ; В=
; В= 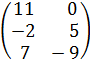

 ; б)
; б)  ; в)
; в) 
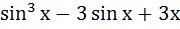
 - 3) при х=1.
- 3) при х=1. ; б)
; б) 
 , В=
, В=  , Е=
, Е=  ,
, В=
В= 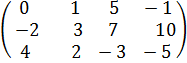
 ; б)
; б)  ; в)
; в) 

 при х=9.
при х=9. ; б)
; б) 



