Предмет деятельности
«Основной, или, как иногда говорят, конституирующей, характеристикой деятельности является её предметность. Собственно, в самом понятии деятельности уже имплицитно содержится понятие ее предмета (Gegenstand). Деятельность может казаться беспредметной, но научное исследование деятельности необходимо требует открытия ее предмета. При этом предмет деятельности выступает двояко: первично – в своем независимом существовании, как подчиняющий себе и преобразующий деятельность субъекта, вторично – как образ предмета, как продукт психического отражения его свойств, которое осуществляется в результате деятельности субъекта и иначе осуществиться не может» [64, с. 142]. Таким образом, предмет деятельности проявляется в двух аспектах: объективном и субъективном. То есть предмет деятельности следует принимать как образ предмета (объекта) и как продукт психического отражения его свойств в результате деятельности субъекта. Таковыми являются, в том числе, определения понятий, формулировки теорем в знаковой и текстовой формах. Определение Арифметическая прогрессия Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d,называют арифметической прогрессией, а число d — разностью арифметической прогрессии [81, с. 102]. Теорема о свойстве медианы равнобедренного треугольника: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой (и высотой)[1] [101, c. 39]. Отдельные конкретные виды деятельности можно различать между собой по любому признаку: по их форме, по способам их осуществления, по их эмоциональной напряженности, по их временной и пространственной характеристике, по их физиологическим механизмам и т.д. Однако главное, что отличает одну деятельность от другой, состоит в различии их предметов. Именно предмет деятельности придает ей определенную направленность, отмечает А.Н. Леонтьев, предмет деятельностиесть ее действительный мотив. Мотив деятельности может быть как вещественным, так и идеальным, как данным в восприятии, так и существующим только в воображении, в мысли. Главное, что за ним всегда стоит потребность, что он всегда отвечает той или иной потребности [63]. Остановимся на специфической математической деятельности учащихся — решении уравнений. Предметом этой деятельности является теория решения уравнений, которую составляют понятия «уравнение», «корень уравнения», задача «решить уравнение». Задача «решить уравнение» требует расширения понятийного аппарата — введения понятий «множество решений уравнения», «равносильные уравнения», а также изучения свойств равносильных уравнений. Ощутить сложность предмета этой деятельности, осознать трудности усвоения этого понятия учащимися позволяет символическая запись определения равносильных уравнений:
Два уравнения Предметом познавательной деятельности учащихся является научное знание или его элементы (понятия, законы, идеи, принципы, правила, входящие в структуру каждой науки), указывает П.И. Пидкасистый, описывая научные основы структурного анализа познавательной деятельности учащегося. При обучении математике предметом познавательной деятельности являются математические понятия (основные и производные), отношения между ними и свойства, представленные в аксиомах и теоремах. В целях данного исследования следует достаточно подробно описать предмет познавательной математической деятельности учащихся средней общеобразовательной школы. К основным понятиям школьного курса математики, как известно, относят понятие числа, множества, элемента множества; к основным отношениям — принадлежность или непринадлежность элемента множеству. Простой пример: рассмотрим букву а русского языка и А – множество букв алфавита русского языка. Если Как видно из приведенных примеров, элементы логики входят в изложение математических знаний, являясь средством математического языка. Наиболее ярко необходимость в применении математического языка видна при изучении школьного курса геометрии, построенного по законам логики. Основные геометрические фигуры (объекты): точка, прямая, плоскость относят к основным (неопределяемым) математическим понятиям. Свойства основных понятий раскрываются в аксиомах (основных свойствах), производным понятиям даются определения. В пропедевтическом курсе математики не все понятия и отношения определяются. Так, например, понятие натурального числа вводится в математике «через абстракцию» [75, с.70] или аксиоматически (аксиомы Пеано) [99]. Такие понятия вводятся посредством поясняющих описаний: в пятом классе натуральное число характеризуется как число, используемое при счете предметов [37, 71 и др.]. Отношения между числами и операции над ними не определяются, а формулируются правила (алгоритмы действий). Свойства производных понятий формулируются в суждениях, различающихся структурой и областью истинности. Утверждение, истинность которого доказана в данной теории, называют теоремой [113]. Таким образом, предмет познавательной математической деятельности учащихся средней общеобразовательной школы составляют математические (в том числе логические) понятия, отношения между понятиями, определения производных понятий, аксиомы и теоремы, алгоритмы и правила. На описании предмета познавательной деятельности при обучении математике более детально остановимся в разделе о дидактических аспектах реализации деятельностного подхода при обучении математике в следующей главе. Завершая описание «научного знания» как предмета познавательной деятельности, снова обратим внимание на процедуру познавательной деятельности, описанную П.И. Пидкасистым. Ученик усваивает «научное знание, которое первоначально выступает в его деятельности как объект познания. Став же достоянием ученика, это знание в его последующей познавательной деятельности выступает в сознании школьника, с одной стороны, уже как сам предмет познавательной деятельности, с другой – как её результат» [98, с. 84]. В результате материализованы цели, предметные действия, операции, способности и возможности личности. С результатом сопряжена оценка и самооценка личности, ее статус в коллективе. Это оставляет большой след в развитии личности, ее побуждений, устремлений, ее действий, ее умений и способностей. Таким образом, деятельность — это подлинный источник развития личности. Это показатель развития, знаний, умений личности не только для окружающих, но и для нее самой, что, пожалуй, более для нее значимо.
|



 .
. Х
Х  Y, где Х
Y, где Х  , Y
, Y  .
.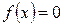 и
и  называются равносильными, еслимножества их корней совпадают. Очевидно, что теория решения уравнений, представленная традиционно в седьмом классе [3, 46 и др.], как предмет деятельности, не обеспечивает создание должной мотивации при ее изучении. К этому моменту учащиеся не владеют даже символическим обозначением функции. Деятельность «решение уравнений» может быть порождена мотивом, истоки которого в её предмете. Следовательно, деятельностный подход при изучении уравнений требует критического анализа предмета специфической деятельности учения. Этому вопросу посвящен пункт 3.1.3 третьей главы монографии.
называются равносильными, еслимножества их корней совпадают. Очевидно, что теория решения уравнений, представленная традиционно в седьмом классе [3, 46 и др.], как предмет деятельности, не обеспечивает создание должной мотивации при ее изучении. К этому моменту учащиеся не владеют даже символическим обозначением функции. Деятельность «решение уравнений» может быть порождена мотивом, истоки которого в её предмете. Следовательно, деятельностный подход при изучении уравнений требует критического анализа предмета специфической деятельности учения. Этому вопросу посвящен пункт 3.1.3 третьей главы монографии. то
то  (d – буква латинского алфавита). Заметим, что уже в этом простейшем описании использовано логическое понятие «высказывание» и использованы логические операции импликации, отрицания и эквиваленции (неявно):
(d – буква латинского алфавита). Заметим, что уже в этом простейшем описании использовано логическое понятие «высказывание» и использованы логические операции импликации, отрицания и эквиваленции (неявно):  . Высказывание
. Высказывание  является истинным,
является истинным, 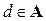 – ложно.
– ложно.


