В.В. Давыдов
Общеизвестно, что деятельность в процессе обучения складывается из двух основных видов: деятельности учителя – преподавания и деятельности ученика – учения. Остановимся на трактовках данных понятий, сформулированных И.Я. Лернером. Преподавание – деятельность по организации усвоения содержания и руководству этим усвоением. Учение – деятельность ученика по организации условий, обеспечивающих усвоение им содержания образования. Обучение людей – «акт взаимодействия учителя и ученика с целью усвоения последним некоторого содержания социального опыта. Процесс обучения – происходящая по определенным объективным законам смена актов обучения, в ходе которой изменяются деятельность учителя и учащихся, а также личные качества учащихся в результате их деятельности» [65, с.12]. Структуру процесса обучения И. Я. Лернер представил таким образом:
СОДЕРЖАНИЕ
П.И. Пидкасистым структурные компоненты обучения представлены аналогичной триадой: содержание образования, деятельность преподавания и деятельности учения [98]. В результате анализа познавательной деятельности учащегося автором выделяется предмет деятельности — «объективированное научное знание или его элементы» [98, с. 84]. Как видно из анализа структуры процесса обучения, компоненты этого процессаобъединяет предмет познавательной деятельности. В методической литературе отмечается, например, что методы познания выступают как элементы «содержания образования — с одной стороны, и как приемы мышления — с другой [113, с.113]. Соотнесение этого факта с триадой П.И. Пидкасистого позволяет утверждать, что методы научного познания принадлежат и к содержанию обучения (научному знанию), и деятельности учения (общие познавательные действия). Итак, как эмпирические, так и логические методы научного познания входят, стало быть, в состав предмета познавательной деятельности. Познавательная деятельность в структуре обучения довольно специфична, поскольку она определяется и особенностями преподавания (деятельностью преподавателя), и спецификой предмета познавательной деятельности. П.И. Пидкасистый особо характеризует предмет – научное знание, которое имеет две стороны: логико-операционную и содержательную. Логико-операционная сторона – это слова, знаки, символы, их структурные связи. Содержательную сторону составляют признаки, свойства, качества, отношения реального мира, т.е. всё то, о чем информируют нас слова, символы и знаки. Таким образом, научное знание имеет свою форму и содержание. Чтобы самостоятельно конструировать знания, надо знать, что (понятие, закон, правило) и как конструировать. Иными словами, обучаемых нужно «учить познавательной деятельности, вооружать их учебно-познавательным аппаратом» [98, с. 89]. Цель данной главы — выделить особенности предмета познавательной деятельности — научного знания — при изучении математики в средней школе. Содержанием учебного предмета «математика» являются факты курса арифметики, алгебры, геометрии и математического анализа. Формой – понятия, аксиомы, теоремы, символы и логические связки, с помощью которых можно представить и раскрыть содержание учебного материала. К логико-операционной стороне курса математики (форме научного знания) относятся, наряду с её логическим строением, определения понятий и их структура, структура аксиом и теорем, виды теорем, доказательство и методы доказательства утверждений. Таким образом, в исследовании реализации деятельностного подхода в процессе обучения математике мы исходим из признания приоритета предмета познавательной деятельности, обеих его сторон (логико-операционной и содержательной) как основы разработки дидактических средств для решения поставленных задач. На наш взгляд, в исследовании проблемы реализации деятельностного подхода при обучении математике недостаточно глубоко использованы сущность и роль логико-операционной стороны научного знания. В данном исследовании, выделяя как главную задачу математического образования школьников формирование у них основных видов деятельности, присущих обучению математике, мы исходим в первую очередь из того, что структура (форма) математического знания должна быть усвоена учащимися так же, как его содержание. Более того, качество усвоения знаний существенно зависит от того, как усвоен процессуальный аспект — форма предмета познавательной деятельности. В традиционном обучении (многовековом опыте) основное внимание было сосредоточено на содержательной стороне научного знания, что привело в конце XX века к противоречиям в обучении, отразившимся, в частности, в утрате интереса к учению значительной части школьников, в резком отставании их от наиболее способных учащихся. Процитируем в связи с этим очень значимое, на наш взгляд, описание П.И. Пидкасистым познавательной деятельности учащегося в условиях информационно-объяснительного (традиционного) обучения и в условиях осуществления деятельностного подхода к обучению. В условиях информационно-объяснительного обучения, когда учитель выступает в основном в роли информатора, познавательная деятельность ученика не может быть предметом обучения, поскольку она сама является следствием поступления информации. Информация поступает – познавательная деятельность совершается; подача её прекращается – прекращается и познавательная деятельность. Для того чтобы научить школьников познавательной деятельности, надо в процессе обучения выделить особые формы и способы действий, с помощью которых они будут усваивать знания. «Определённая последовательность действий является не только способом раскрытия содержания понятий, но и предметом усвоения» [98, с. 89]. Научные знания могут стать достоянием индивида только через его активную практическую и мыслительную деятельность. Для этого нужен познавательный инструментарий, помогающий проникать в сущность предмета познания. Он представляет собой совокупность логических средств добывания знаний. Обучение учащихся «способам выполнения познавательных действий и успешное вооружение их необходимым и специфическим для каждого учебного предмета инструментарием логических операций связаны, прежде всего, с соответствующей организацией учебной деятельности школьника в процессе обучения» [Там же, с.90]. Аналогичные выводы следуют из работ Н.Ф. Талызиной. Например, в статье «Что значит знать?» автор, анализируя отношения между знаниями и познавательными действиями человека, отмечает как важную методическую задачу «определить те виды деятельности, которым необходимо учить при усвоении знаний» [127, с. 98]. Наконец, исследование проблемы развития познавательной самостоятельности учащихся в обучении математике [106] и многолетний опыт работы учителем математики убеждают, что только целенаправленное формирование действий, присущих математической деятельности, приводят к положительным результатам обучения. Такими действиями в обучении математике являются, например, изучение текста задачи (анализ как разложение целого на части), обнаружение закономерности и формулировка нового утверждения (неполная индукция, обобщение), поиск плана решения задачи и доказательства теоремы (метод восходящего анализа), построение доказательства теоремы, осуществление плана решения задачи (дедуктивное рассуждение). Наблюдения за работой студентов показывают, что в проблемной ситуации их, как правило, может выручить только предшествующий опыт решения данной задачи. В отсутствии такового студенты математического факультета, к сожалению, проявляют беспомощность. Они стараются применить теорему, в которой идет речь об объектах, входящих в условие задачи; выполнить возможные, часто встречаемые в аналогичных ситуациях дополнительные построения, но все безуспешно. Дело в том, что при этом студентами используются действия (приемы), основанные на синтетическом методе, применяемом для оформления результатов решения задачи. Часто при изучении методов научного познания с третьекурсниками, а также при изучении сущности деятельностного подхода к обучению со студентами пятого курса педагогического университета для мотивации их учения предлагаются следующие две задачи. Задача 1. Найдите сумму дробей: На решение задачи отводится столько времени, чтобы можно было осуществить поиск и решение задачи. Из немногочисленных гипотез поисковой деятельности появляется правдоподобный результат: значение суммы равно 1. Остальные предположения — попытки угадывания, без должного анализа и индуктивных поисков. Как правило, приходится резюмировать, что без посторонней помощи задача студентами (группа в 20-30 человек) не может быть решена в данный момент. Причина — отсутствие навыков индуктивного поиска. Студенты привыкли получать готовые знания, а не открывать их. Оказалось, это еще и школьная привычка. Задача 2. В треугольнике АВС угол А равен 30 °, а угол В равен 50 °. Докажите, что верно равенство: с² = b· (a + b),где а, b, с – стороны треугольника. Первое действие процесса решения задачи — изучение задачи, выражающееся во внешней деятельности построением чертежа и записью условия и требования задачи, выполняется каждым студентом. Это общее действие, основанное на простом анализе текста, многократно повторяемое в процессе обучения, формируемое при доказательстве теорем и решении многих типов математических задач, а также в решении задач по физике, химии, как правило, не вызывает затруднений. Следующее действие — поиск плана решения, также часто используемое в решении задач, в данной задачной ситуации обнаруживает полное отсутствие привычки выполнять целенаправленный поиск: осуществлять рассуждение, например, восходящим анализом. И студенты, и учителя математики (часто доводится работать на курсах повышения квалификации), опираясь на многолетний опыт, память, выполняя поиск плана решения данной задачи, записывают и пытаются применить теорему косинусов (схожие составляющие с требованием задачи), теорему синусов (сторона а — угол А равен 30 °; сторона b — угол В равен50 °), свойство катета прямоугольного треугольника, лежащего против угла в 30 °, теорему Пифагора (проводя высоту треугольника АВС), т.е. рассуждают сообразно синтетическому методу и … заходят в тупик. План решения задачи не появляется. Обсуждение создавшейся проблемной ситуации показывает, что рассуждение восходящим анализом в большинстве случаев не выполнялось решающими задачу. Привычка рассуждать по схеме восходящего анализа в проблемной ситуации не сформирована вообще. В подобных ситуациях человек привык идти путем проб и ошибок, используя предшествующий опыт. В теории обучения математике вопросу применения метода восходящего анализа уделяется большое внимание [20, 75, 113, 138 и др.], ему обучают будущих учителей, формируют умение задавать вопросы учащимся в соответствующих ситуациях. Но не обсуждается проблема формирования умения учащихся задавать себе вопросы, целенаправленные, приводящие к открытию способа решения задачи, плана доказательства теоремы. Возможно, что причинами подобной ситуации являются эвристический характер метода восходящего анализа, трудности в формировании его у школьников в связи с временными затратами и профессионализмом учителя, отсутствие установки на формирование привычки выполнять поиск решения задачи «от главного вопроса к условию», а не синтетическим методом «по образцу». До сих пор в методической литературе часто используется прием наводящего (по существу подсказывающего) вопроса учителя. Подсказывающими являются и вопросы актуализации знаний перед решением задачи. Практика обучения решению задач и доказательству теорем убеждает в том, что от проблемных ситуаций, так свойственных изучению математики, часто уходят, заботясь о темпе работы на уроке, о количестве решенных задач, а не о развитии мышления учащихся. Таким образом, для обучения школьников познавательной математической деятельности нужно: – выделить основные виды математической деятельности учащихся, с помощью которых они усваивают знания; – описать структуры выделенных основных видов деятельности школьников при изучении математики; – разработать технологию формирования этих видов деятельности у учащихся общеобразовательных учреждений. Сформулированные выше принципы являются следствием принятого нами положения о сущности предмета познавательной деятельности учащихся. Они и составляют основу методической реализации деятельностного подхода к обучению математике в средней общеобразовательной школе. Для описания практического осуществления деятельностного подхода при обучении математике нами поставлена задача: обосновать и описать компоненты структуры деятельностей «введение понятия», «изучение утверждений», «процесс решения задачи» (глава 4, с. 69). Кроме того, в ходе изучения сущности предмета познавательной деятельности учащихся, исследуя роль классификации при введении понятия, обращает на себя внимание следующая классификация понятия «выражение» [67, с.174] (см. ниже, рис. 6). На наш взгляд, она имеет принципиальное значение с точки зрения предмета деятельности при обучении математике. В частности, она полезна для осуществления системного отбора содержания обучения. Для изучения линейных неравенств, числовых функций и их свойств необходимы свойства числовых неравенств (выражений без переменной со знаком отношения), а для изучения уравнений — свойства числовых равенств. Числовые равенства и неравенства, как следует из классификационной схемы, составляют множество выражений – высказываний.
Рис. 6 В содержание обучения традиционно входит понятие «выражение» и его объем: выражения без переменной и выражения с переменной. Однако если выражения «имя числа» (без переменной и без знака отношения) изучаются в пятом, шестом и начале седьмого класса, то «высказывания» в явном виде в действующих учебниках [3, 79 и др.] не изучаются, а числовые неравенства вводятся в изучение только в конце восьмого класса [4, 80 и др.]. Опыт изучения числовых неравенств в седьмом классе (с введением определения понятия числового неравенства на основе отношений «больше», «меньше» и др.) в теме «Что такое математический язык», «Что такое математическая модель» [79, с. 16, 17] оказался весьма удачным. Тем более что изучение числовых промежутков предусмотрено учебником алгебры в седьмом классе [Там же, с. 98]. Теоремы о свойствах числовых неравенств наглядны, имеют импликативную структуру, например: «если a > b, то b < a». Их доказательства просты, не требуют много времени на изучение. А главное, свойства числовых неравенств в этом подходе являются первыми теоремами курса алгебры и позволяют вести обучение доказательству в начале изучения алгебры. Другое важное обстоятельство состоит в том, что на примере теорем о свойствах числовых неравенств можно формировать знания учащихся о предмете деятельности: о понятии «теорема», «структура теоремы», «доказательство». Наконец, в содержательном плане удается ввести определение возрастающей и убывающей функции, а свойство монотонности линейной функции [79, с. 122], функции
|



 УЧИТЕЛЬ
УЧИТЕЛЬ ОБРАЗОВАНИЯ УЧЕНИК
ОБРАЗОВАНИЯ УЧЕНИК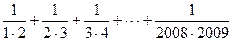 (задача школьного или районного тура математической олимпиады).
(задача школьного или районного тура математической олимпиады).
 [Там же, с. 133] учащиеся могут уже самостоятельно доказать.
[Там же, с. 133] учащиеся могут уже самостоятельно доказать.


