Характеристика структурных компонентов деятельности
1.2.1. Структура категории «деятельность» Деятельность есть «система, имеющая строение, свои внутренние переходы и превращения, свое развитие»[64, с. 141]. Содержание понятия «деятельность» раскрывается А.Н. Леонтьевым посредством категорий мотивационно-ориентировочного и процессуального циклов структуры. Мотивационно-ориентировочный аспект деятельности составляют потребности, мотив, цель и условия, а процессуальный — действие, операции [31]. «Подобно тому, как понятие мотива соотносится с понятием деятельности, понятие цели соотносится с понятием действия» [64, с. 153]. Структуру понятия деятельность, описание компонентов которой приведено ниже, можно представить в виде схемы – структуры (рис. 1).
Всякая деятельность состоит из действий (поступков), основанных на тех или иных побуждениях. Поэтому потребность может выступать «как внутреннее условие, как одна из предпосылок деятельности. С другой стороны, потребность выступает фактором, который направляет и регулирует конкретную деятельность субъекта в предметной среде» [Там же, с. 144]. В первом случае потребность выступает как состояние нужды организма и сама по себе не может вызвать никакой определённо направленной деятельности. Её функция ограничивается возбуждением двигательной сферы, которое проявляется в ненаправленных поисковых движениях. Например, потребность может быть физиологической. Человек нуждается в пище, воде. Однако для удовлетворения потребности в пище он должен выполнять действия, которые непосредственно на овладение пищей не направлены. Целостность деятельности выступает как единство целей, на которые она направлена, и мотивов, из которых она исходит. При этом мотивы и цели деятельности, в отличие от мотивов и целей отдельных действий, носят обобщённый характер, выражая общую направленность личности. В самом начале школьной жизни у ребёнка ещё нет потребности в теоретических знаниях как психологической основе учебной деятельности. Эта потребность возникает в процессе усвоения им элементарных теоретических знаний при совместном с учителем выполнении простейших учебных действий, направленных на решение соответствующих учебных задач [31]. Существуют своеобразные отношения между потребностями, мотивом, действиями, операциями. Мотив деятельности может переходить в цель действия (на рисунке показано стрелочкой), тогда деятельность обращается в действие. Или, наоборот, сдвиг цели действия на мотив трансформирует действие, которое может развернуться в деятельность, имеющую теперь самостоятельный мотив (сознательный мотив) [63]. В таких взаимопереходах рождаются новые деятельности, происходит переход от одной стадии деятельности к другой. Подобным взаимопереходам обязано и становление мотивации познавательной деятельности. Это важнейшее положение деятельностной теории учения многократно иллюстрируется примерами, приведенными в третьей главе данной работы. Действие классификации понятия, входящее в деятельность «введения понятия» (с. 78), раскрывает перед учащимися перспективу изучения курса математики (алгебры, геометрии). Выполнение действия «осуществление доказательства» или «осуществление плана решения задачи» соответственно в видах математической деятельности учащихся «изучение утверждения» или «процесс решения задачи» в форме дедуктивного рассуждения (с. 89, 90 и др.) наглядно иллюстрирует значение изученной ранее теории, показывает, как следует изучать предмет, чтобы овладеть математическими знаниями. Оба отмеченных примера с разных сторон, различными средствами позволяют учителю аргументированно убедить любого школьника в значимости изучения математики, а также в том, что овладеть этим предметом может каждый ученик, правда, уровень усвоения будет зависеть от того, какое место занимает он в системе ценностей ребенка. Мотивация учения, реализуемая посредством основных видов математической деятельности учащихся, представляет собой воплощение идеи воспитания школьников средствами своего предмета — образования с помощью математики [54]. Опыт показывает, что формирование основных видов деятельности учащихся при обучении математике способствует становлению их мотивации. Тот или иной мотив побуждает человека к постановке задачи, к выявлению той цели, которая, будучи представлена в определённых условиях, требует выполнения действия, направленного на создание или получение предмета, отвечающего требованиям мотива и удовлетворяющего потребность. Способ и характер выполнения действия, направленного на решение задачи, определяется её целью, в то время как условия задачи определяют конкретные операции, входящие в данное действие. Деятельность может утратить свой мотив и превратиться в действие, а действие при изменении его цели может превратиться в операцию. Подвижность составляющих деятельности выражается и в том, что каждая из них может стать дробной или, наоборот, будет включать в себя другие [63]. Проиллюстрируем сказанное примером деятельности «выведение следствий». В исследованиях Н.Ф. Талызиной по деятельностной теории учения младших школьников выведение следствий выступает как «общий вид познавательной деятельности», как «прием логического мышления» [128, с. 56]. Как известно, «выведением следствий» называется действие, состоящее в получении «следствий из факта, что объект принадлежит к классу объектов, охарактеризованных определением» [68, с. 43]. Ясно, что при усвоении нового математического понятия, его определения, упражнения на выведение следствий являются обязательными. При этом «выведение следствий» в структуре деятельности «введение понятия» выступает как действие (см. с. 78). Это действие утрачивает свою цель в таких видах деятельности при обучении математике, как «изучение утверждения» и «процесс решения задачи», обращаясь в операцию. Покажем это на примере утверждения о медиане равнобедренного треугольника, проведенной к основанию.
Таблица 1 Доказательство:
четыре раза — при построении первого, третьего, пятого и шестого силлогизмов (табл. 1). Суждения, полученные на основе подведения объекта под определение понятия, являются результатом умозаключений — выведения следствий.
|

 Рис. 1
Рис. 1
 B
A M C
B
A M C
 — равнобедренный,
[ АС ] — основание,
— равнобедренный,
[ АС ] — основание,  [ ВМ ] — медиана.
Доказать: [ ВМ ] — биссектриса
[ ВМ ] — медиана.
Доказать: [ ВМ ] — биссектриса  и
и 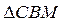 ,
[ АВ ]=[ ВС ], Ð А =Ð С, [ АМ ]=[ МС ]
,
[ АВ ]=[ ВС ], Ð А =Ð С, [ АМ ]=[ МС ]



