Основные правила вычисления вероятностей сложных событий
Ниже приведены основные правила, позволяющие определить вероятность появления сложного события на основании известных вероятностей составляющих его более простых событий. 1. Вероятность достоверного события равна единице:
2. Вероятность объединения (суммы) несовместных событий равна сумме их вероятностей:
Эти два равенства являются аксиомами теории вероятностей, т. е. принимаются в качестве исходных, но требующих доказательства свойств вероятностей. На их основе строится вся теория вероятностей. Все остальные, приведенные ниже без доказательств формулы могут быть выведены из принятых аксиом. 3. Вероятность невозможного события равна нулю:
4. Вероятность события, противоположного событию А, равна
Формула (4.5) оказывается полезной на практике в тех случаях, когда вычисление вероятности непосредственно события А затруднительно, в то время как вероятность противоположного события находится просто (см. ниже п. 9). 5. Теорема сложения вероятностей. Вероятность объединения произвольных событий равна сумме их вероятностей за вычетом вероятности произведения событий:
Для несовместных событий 6. Условная вероятность. Если требуется найти вероятность события В при условии, что произошло некоторое другое событие А, то такую ситуацию характеризуют с помощью условной вероятности
В тех случаях, когда события А и В несовместны, 7. Определение условной вероятности в виде (4.7) дает возможность записать следующую формулу для вычисления вероятности произведения событий(теорема умножения вероятностей)
8. Поскольку вероятность события А (или В) для независимых событий по определению не изменяется при появлении другого события, то условная вероятность
Теорема умножения вероятностей для независимых событий записывается следующим образом:
т. е. вероятность произведения независимых событий равна произведению их вероятностей. 9. Вычислим вероятность появления хотя бы одного события в n испытаниях А – появление в n испытаниях хотя бы один раз интересующего нас события.
А 1 – интересующее нас событие появлилось в первом испытании. А 2 – интересующее нас событие появлилось во втором испытании. …. А n – интересующее нас событие появлилось в n -ом испытании.
10. Формула полной вероятности. Если событие А может произойти только при появлении одного из несовместных событий Н1, Н2, …, Нn, то
|

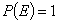 . (4.2)
. (4.2)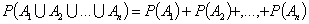 (4.3)
(4.3)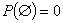 . (4.4)
. (4.4)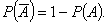 (4.5)
(4.5)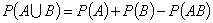 . (4.6)
. (4.6)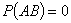 и формула (4.6) переходит в (4.3).
и формула (4.6) переходит в (4.3).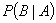 . Условная вероятность равна отношению вероятности произведения событий А и В к вероятности события А:
. Условная вероятность равна отношению вероятности произведения событий А и В к вероятности события А: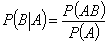 (4.7)
(4.7)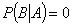 .
.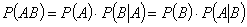 (4.8)
(4.8)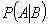 совпадает с вероятностью события А, а условная вероятность
совпадает с вероятностью события А, а условная вероятность 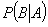 — с Р(В). Вероятности Р(А) и Р(В) в отличие от условных вероятностей называются безусловными.
— с Р(В). Вероятности Р(А) и Р(В) в отличие от условных вероятностей называются безусловными.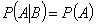 ,
, 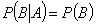 , (4.9)
, (4.9)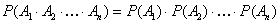 , (4.10)
, (4.10) – интересующее нас событие не появлилось в n испытаниях ни разу.
– интересующее нас событие не появлилось в n испытаниях ни разу.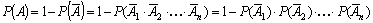 (4.11)
(4.11)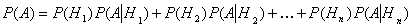 . (4.12)
. (4.12)


