При построении сети электросвязи обычно считают, что одним из наиболее важных показателей развития сети является телефонная плотность (количество телефонов на 100 жителей). Как показывают проведенные исследования, объем информационных потоков возрастает пропорционально квадрату уровня национального дохода на душу населения. Следовательно, значение телефонной нагрузки, создаваемой общим информационным потоком страны, может быть выражено в следующем виде:
 ,(12.4.3)
,(12.4.3)
где с — национальный доход на душу населения; V — число жителей страны; k — коэффициент пропорциональности.
Изменение (прирост) нагрузки в зависимости от роста национального дохода можно записать в виде ΔА=2k*c*N*Δc, а относительное изменение нагрузки равно:
 ΔA/A=2k*c*N*Δc/A=2*Δc/c=2δ;,(12.4.4)
ΔA/A=2k*c*N*Δc/A=2*Δc/c=2δ;,(12.4.4)
где δ – относительный прирост национального дохода.
Из этого следует, что относительный прирост нагрузки общего информационного потока пропорционален удвоенному относительному приросту национального дохода δ. Пользуясь этой закономерностью, в соответствие с выражением(12.4.2), можно прогнозировать объем общего информационного потока и нагрузки, им создаваемой, на период t лет исходя из соотношения:
At=A1 (1+2δ)t, (12.4.5)
где A1 – значение нагрузки в начале срока прогнозирования; At - то же в конце срока прогнозирования;t – продолжительность периода прогнозирова-ния.
Для выражения закономерностей изменения телефонной плотности, в зависи-мости от условий, используются различные математические модели. Для сравнительно короткого периода времени можно использовать линейную зависимость телефонной плотности от времени
σt = σ +k1t, (12.4.6)
где σt — телефонная плотность через t лет; σ — начальная телефонная плотность; k1 — ежегодный прирост телефонной плотности.
Если считать ежегодный относительный прирост a телефонной плотности постоянным и не превышающим определенных величин, то телефонная плотность будет увеличиваться по экспоненте с соотношением
 (12.4.7)
(12.4.7)
Зависимость не может быть использована в течение неограниченного периода времени, так как σt стремится к бесконечности. Однако во многих случаях, когда телефонная плотность мала, экспоненциальная зависимость является хорошей моделью для целей прогнозирования. Если считать, что существует некоторый предел σмах, к которому стремится телефонная плотность, то математической моделью такой зависимости, имеющей предел, может быть, например, кривая Гомпертца, описываемая выражением:
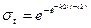 (12.4.8)
(12.4.8)
где k2 и t2 — постоянные величины.
При малых значениях t соотношении это близко к (12.4.7), поэтому начальный рост телефонной плотности происходит по экспоненте. После достижения величиной t значения t2, при котором плотность σt =σмах /e, скорость роста уменьшается. При стремлении t к бесконечности кривая стремится к насыщению (σt =σмах).
Еще одной математической моделью, которая также стремится к насыщению, является логистическая кривая. При ее получении предполагается, что вероятность того, что житель, не являющийся абонентом, превратится в абонента в течение рассматриваемого года, пропорциональна числу имеющихся абонентов и числу жителей, еще не ставших абонентами. Логистическая кривая описывается соотношением:
 . (12.4.9)
. (12.4.9)
Для малых значений t она практически совпадает с экспонентой. После дости-жения t значения t2 скорость роста замедляется, и при t, стремящейся к беско-нечности, значение плотности стремится к своему значению насыщения
(σt = σmax).
Телефонная плотность во многих странах с большой точностью подчиняется логистической кривой.

 ,(12.4.3)
,(12.4.3) ΔA/A=2k*c*N*Δc/A=2*Δc/c=2δ;,(12.4.4)
ΔA/A=2k*c*N*Δc/A=2*Δc/c=2δ;,(12.4.4) (12.4.7)
(12.4.7)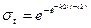 (12.4.8)
(12.4.8) . (12.4.9)
. (12.4.9)


