Аналитический способ. При наличии прямоугольных координат X и Y вершин n -угольника его площадь можно вычислить по формулам аналитической геометрии; выведем одну из таких формул.
При наличии прямоугольных координат X и Y вершин n -угольника его площадь можно вычислить по формулам аналитической геометрии; выведем одну из таких формул. Пусть в треугольнике ABC координаты вершин равны X1, Y1 (A), X2, Y2 (B) и X3, Y3 (C) - рис.6.2.
Рис.6.2 Из вершин треугольника опустим перпендикуляры на оси координат и обозначим их длину, как показано на рис.6.2. Площадь треугольника P будет равна сумме площадей двух трапеций I(aABc) и II(bBCc) за вычетом площади трапеции III(aACc) P=PI+PII-PIII. (6.9) Выразим площадь каждой трапеции через ее основания и высоту: PI=0.5(X1+X2)*(Y1-Y2); Чтобы избавиться от множителя 0.5, будем вычислять удвоенную площадь треугольника. Выполним умножение, приведем подобные члены, вынесем общие множители за скобки и получим: 2*P=X1*(Y2-Y3)+X2*(Y3-Y1)+X3*(Y1-Y2) или в общем виде: 2*P=∑[Xi*(Yi+1-Yi-1)] 2*P=∑[Yi*(Xi-1-Xi+1)]
В этой формуле индекс "i" показывает номер вершины треугольника; индекс "i" означает, что нужно брать следующую или предыдущую вершину (при обходе фигуры по часовой стрелке). Если при группировке членов выносить за скобки Y1, то получится формула:
Вычисления по обоим формулам дают одинаковый результат, поэтому на практике можно пользоваться любой из них. Хотя формулы (6.11) и (6.12) выведены для треугольника, нетрудно показать, что они пригодны для вычисления площади любого n - угольника. Оценка точности площади. В большинстве случаев участки на местности имеют форму неправильного n - угольника, причем количество вершин многоугольника n может быть от 30 до 20 и более. Площадь таких участков вычисляют аналитическим способом по прямоугольным координатам вершин, которые, в свою очередь, определяют в результате обработки геодезических измерений. При этом для каждой вершины многоугольника получают координаты и ошибку ее положения относительно исходных пунктов, задающих систему координат на местности. Выведем формулу для оценки площади многоугольника по известным внутренним углам, длинам его сторон и ошибкам положения mti его вершин. На рис.6.3 изображен фрагмент многоугольника с вершинами i-1, i, i+1, i+2 и сторонами li-1,li,li+1. Проведем на вершинах i и i+1 окружности радиусами mti и mt(i+1) и построим биссектрисы углов βi и βi+1. Затем восстановим перпендикуляры к стороне li и найдем проекции отрезков mti и mt(i+1) на эти перпендикуляры:
Рис.6.3 Построим трапецию, основаниями которой являются отрезки mi и mi+1, а высотой - сторона li и найдем площадь этой трапеции ΔPi. Как известно, площадь трапеции равна произведению полусуммы оснований на высоту, а поскольку основаниями трапеции являются проекции ср.кв. ошибок, то вместо полусуммы нужно взять квадратичную полусумму оснований; таким образом,
где c = Sin(β/2). Площадь трапеции, построенной на одной стороне многоугольника, является частью ошибки площади всего многоугольника; выполнив квадратичное суммирование площадей ΔPi по всем сторонам, получим:
или
Из формулы (6.16) можно получить формулу средней квадратической ошибки площади правильного многоугольника с одинаковой ошибкой положения mt всех его вершин: mP=an * mt * L, (6.17) где: L - периметр многоугольника, его значения:
Формула (6.17) является базовой и при оценке площади неправильных n-угольников, для которых ошибка площади mp оказывается лишь на несколько процентов больше, чем для правильного n - угольника. Так, если площадь неправильного n - угольника при том же периметре в два раза меньше площади правильного n-угольника, то ошибка его площади увеличивается лишь на 20 %. При неодинаковых ошибках положения вершин многоугольника в формуле (6.17) достаточно вместо mt поставить mt(ср). Примером применения формулы (6.17) является оценка площади участков, координаты вершин которых получены с топографических планов. Например, для плана масштаба 1:2000 ошибку положения точек можно принять равной mt = 0.50 мм * M = 1 м (при условии, что основа плана достаточно жесткая и ее деформацией можно пренебречь). При площади участка 0.12 га и количестве вершин n=4 (5 или 6) средняя квадратическая ошибка его площади при правильной форме (периметр L = 140 м) будет равна 35 кв.м, а при неправильной форме (периметр L>140 м) она может достигать 40 кв.м. Другим примером применения формулы (6.17) может служить оценка площади многоугольника, координаты вершин которого получены из полярной засечки, выполненной с одного пункта-станции. При использовании точных приборов (электронных тахеометров или систем GPS) доля ошибок измерений в ошибке положения точек значительно меньше доли ошибки их фиксации mф на местности. Приняв mti= mф, можно использовать формулу (6.17) для любых способов получения координат вершин многоугольника. Площадь правильного n-угольника можно выразить через его периметр:
И из формулы (6.17) получить формулу относительной ошибки площади:
где
Например:
Таким образом, для приближенной оценки площади 3-4-5-6- угольника в аналитическом способе можно применять формулу: mp/P=4* mt/L; (6.21) ошибка этой формулы может достигать 15% - 20% для участков, форма которых заметно отличается от формы правильного n -угольника.
|


 (6.11)
(6.11) (6.12)
(6.12) (6.13)
(6.13) (6.14)
(6.14)
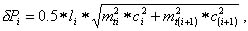 (6.15)
(6.15)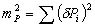
 (6.16)
(6.16)
 (6.18)
(6.18) (6.19)
(6.19) (6.20)
(6.20)


