Понятие о редуцировании площади участка
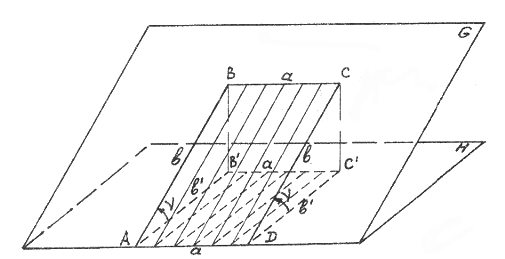
Участок местности в общем случае имеет неровную поверхность, и поэтому в геодезии различают площадь физической поверхности участка Pф и площадь проекции участка на горизонтальную плоскость P; ясно, что Pф > P. Пусть участок прямоугольной формы расположен на плоскости G, имеющей угол наклона ν (рис.6.9). Площадь прямоугольника ABCD на плоскости G будет равна: Pф = a * b, (6.28) где a, b - стороны прямоугольника. Площадь горизонтальной проекции этого же прямоугольника равна: P = a * b' = a * b * Cos (ν) или P = Pф * Cos(ν). 1 (6.29)
Рис.6.9 Далее можно написать: P = Pф - ΔP, (6.30) где ΔP = 2 * Pф * Sin2(ν/120). (6.31) Таким образом, относительное искажение площади участка ΔP/Pф зависит только от угла наклона; при этом форма участка и его расположение в плоскости G не влияют на величину искажения. В следующей таблице приведены численные значения относительного искажения площади участка для разных углов наклона ν. Таблица 6.2
Если угол наклона плоскости G неизвестен, то абсолютное искажение площади можно получить по известным координатам и отметкам поворотных точек контура участка, выполнив следующие операции:
P = 0.5 * Σ [ Xi * (Yi+1 - Yi-1)],
где hi - превышение по i - той стороне,
X'1 = X1, Y'1 = Y1, и вычислить координаты всех остальных поворотных точек контура в этой системе по формулам: X'i+1 = X'i + di * Cos(αi),
Pф = 0.5 * S[X'i * (Y'i+1 - Y'i-1)],
ΔP = Pф - P. Если поверхность участка имеет произвольно сложную форму, то участок нужно разделить на t частей желательно треугольной формы, каждая из которых имеет постоянный угол наклона к горизонту, вычислить искажения площади для всех t частей и найти их сумму. При делении участка нужно соблюдать следующие правила:
Координаты и отметки этих точек можно определять по топографической карте или плану.
|

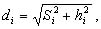 (6.32)
(6.32)


