Последовательность применения основных статистических методов
Метод группировок 1. Сформулировать цель метода группировок. 2. Отобрать группировочный признак, по которому единицы исследуемой совокупности будут распределены на группы. 3. Определить число групп и величину интервала с использованием специальных формул. Построить ранжированный и интервальный ряды распределения по группировочному признаку. 4. Осуществить сводку статистических данных, предварительно наметив статистические показатели, необходимые для расчета результативных показателей в образованных группах. При этом следует выбирать наиболее оптимальную форму расчёта результативных показателей с учётом исходной информации (по формулам средней арифметической простой, средней арифметической взвешенной или средней гармонической). 5. По данным разработочной таблицы для сводки данных составить групповую таблицу, в которой каждую группу охарактеризовать вышеуказанными показателями. Изучить их связь с группировочным признаком и между собой и на этой основе произвести укрупнение. Укрупнение производят также, если соседние группы являются малочисленными. Такая промежуточная группировка позволяет оценить состояние и качественные особенности каждой группы и выделить крупные, типические группы. Новых, объединенных групп должно быть не более 3-4. 6. Построить групповую таблицу, содержащую окончательную аналитическую группировку. В подлежащем таблицы будут объединенные группы, полученные в пункте 5, и итог в целом по совокупности. В сказуемом таблицы – результативные показатели, намеченные для характеристики групп. 7. Сделать выводы по данным групповой таблицы. Корреляционно-регрессионный метод 1. Сформулировать цель корреляционно-регрессионного метода. Эта цель реализуется посредством парной и множественной корреляции. 2. Сформировать совокупность для проведения корреляционно-регрессионного анализа. Осуществить проверку исходной информации на однородность и нормальность распределения по факторным и результативному признакам. Обосновать правомерность применения корреляционных методов (собственно- корреляционные или непараметрические). 3. В случае применения собственно-корреляционных методов установить форму связи между изучаемыми признаками. Эта задача предварительно решается путем построения и анализа графика зависимости (поля корреляции). При построении графика на оси абсцисс располагаются значения факторного признака, а на оси ординат – значения результативного признака. По расположению точек на графике установить форму связи (прямо– или криволинейную) между изучаемыми признаками и выбрать показатель для установления степени тесноты связи (коэффициент или индекс корреляции). Если связь прямолинейная, то рассчитывается коэффициент корреляции. Если связь криволинейная, то степень тесноты связи измеряется индексом корреляции (теоретическим корреляционным отношением). Если относительно формы связи выдвинуты различные теоретические гипотезы, а по виду графика трудно судить о том, какой из этих гипотез наиболее соответствуют фактические данные, то в этом случае строятся и решаются уравнения регрессии с различными формами связи. Затем с помощью специальных статистико-математических критериев оценивается их адекватность, и выбирается та форма связи, которая обеспечивает наилучшую аппроксимацию (приближение) и достаточную статистическую достоверность и надёжность. 4. Рассчитать линейный коэффициент корреляции или индекс корреляции по соответствующим формулам; оценить их значимость с помощью t-критерия Стьюдента или (и) F- критерия Фишера. Исчислить коэффициент или (и) индекс детерминации. Сделать выводы. 6. Построить уравнение (уравнения) регрессии, определить и интерпретировать его (их) параметры. Рассчитать коэффициенты эластичности. 7. Произвести оценку уравнения (уравнений) регрессии на адекватность. 8. В случае высокой статистической надежности уравнений регрессии осуществить прогнозирование уровня результативного показателя путем подстановки в уравнений ожидаемых (или оптимальных) значений факторных показателей.
Индексы Цель индексного метода: определить абсолютное и относительное изменение исследуемого явления в отчётном периоде по сравнению с базисным периодом под влиянием соответствующих факторов, построив мультипликативные и аддитивные факторные индексные модели. Ряды динамики 1. Цель метода рядов динамики: характеристика интенсивности изменений в уровнях исследуемого показателя от года к году, выявление основной тенденции (тренда) изменения уровней в анализируемом периоде и краткосрочное (на 2-3 года) прогнозирование данного явления. 2. Рассчитать цепные, базисные и средние показатели ряда динамики. Результаты расчетов оформить в таблице и по средним показателям динамического ряда сделать выводы. 3. Провести механическое выравнивание ряда динамики с целью выявления основной тенденции, используя прием трехлетней скользящей средней. Результаты выравнивания представить в таблице. 4. Изобразить графически фактические и сглаженные методом скользящей средней уровни динамического ряда на одном рисунке. Используя графический метод, осуществить выбор уравнения тренда для последующего аналитического выравнивания ряда динамики. В ряде случаев, когда затруднительно выбрать единственную функцию, для выравнивания берутся несколько конкурирующих моделей тренда (например, уравнения прямой и параболы 2-го порядка), а затем на основе значения статистико-математического критерия адекватности определяют, какое из уравнений наиболее полно отражает характер изменения изучаемого явления за исследуемый период, т.е., как близко аналитическая функция огибает все значения исходного ряда. 5. Осуществить синтезирование модели (моделей) тренда. Расчет параметров уравнения тренда проводится способом наименьших квадратов, при котором строится и решается система нормальных уравнений. Рассчитать теоретические уровни динамического ряда и отклонения между фактическими и теоретическими уровнями для расчёта коэффициента аппроксимации. Вспомогательные расчёты оформить в таблице. Изобразить теоретические уровни графически на предыдущем рисунке. 6. Рассчитать коэффициент аппроксимации (относительную ошибку аппроксимации) и на его основе произвести оценку точности модели (моделей) тренда. При наличии нескольких моделей выбирается уравнение тренда, имеющее наименьшую ошибку аппроксимации. На основе выбранного уравнения тренда определить тип развития исследуемого явления и сделать вывод об общей тенденции изменения уровней ряда динамики в изучаемом периоде. 7. Вычислить показатели колеблемости уровней динамического ряда. Сделать выводы. 8. В рамках III раздела курсовой работы определить точечный прогноз путём подстановки в синтезированное уравнение тренда условного обозначения прогнозируемого года. 9. Осуществить интервальный (доверительный) прогноз уровня динамического ряда по формуле:
у и n – число уровней ряда; m- число параметров в уравнении тренда.
|

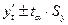 , где
, где - точечный прогноз, рассчитанный по уравнению тренда;
- точечный прогноз, рассчитанный по уравнению тренда;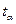 - табличное значение t- критерия Стьюдента при заданном уровне значимости;
- табличное значение t- критерия Стьюдента при заданном уровне значимости;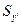 - среднее квадратическое отклонение от тренда (стандартная ошибка аппроксимации):
- среднее квадратическое отклонение от тренда (стандартная ошибка аппроксимации):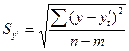 , где
, где


