Процессах
Взаимосвязь изобарной (Сp) и изохорной (Сv) теплоемкостей для n молей идеального газа имеет вид: Cp - Cv = nR, (1.5) где R – универсальная газовая постоянная. Сp и Сv определяются соотношениями: Cv = (¶q/¶T) v = (¶U/¶T)v; (1.6) Cp = (¶q/¶T) p = (¶H/¶T)p; (1.7) и называются истинными теплоемкостями в отличие от средней
Различают молярную (атомную) и удельную теплоемкость. Размерности теплоемкостей: Молярная [C] = Дж/(моль*К); Удельная [С] = Дж/(г*К). Для идеального одноатомного газа: Сv = (3/2)R. (1.9) Для двухатомного газа: Cv = (5/2)R. (1.10) Для трех- и многоатомных газов: Cv = 3R. (1.11) Твердые простые тела подчиняются часто правилу Дюлонга-Пти: Cv»Cp = 3R. (1.12) Выражения (1.9) – (1.12) справедливы для одного моля вещества. Зависимость теплоемкости от температуры обычно выражают эмпирическими (интерполяционными) формулами в виде степенных рядов: C = a + bT + cT2 + dT3; (1.13) С = a + bT + c¢T-2. (1.14) Формулу (1.13) применяют для органических веществ, (1.14) – для неорганических. Коэффициенты a, b, c, d в выражениях (1.13) и (1.14) имеют различное значение и справедливы в данном интервале температур (значения a, b, c, d, c¢ приведены в термодинамическом справочнике). Среднюю теплоемкость по истинной можно определить следующим образом:
и наоборот: C = d[ Количество теплоты, затраченное на нагрев n молей вещества определяется из соотношений: qv = n qp = n Первый закон термодинамики широко применяется для расчета тепловых эффектов в химических реакциях. Согласно закону Гесса (основной закон термохимии), тепловой эффект реакции не зависит от пути процесса, а определяется начальным и конечным состояниями системы, при условии, что объем и давление остаются постоянными, а температуры в конце и начале процесса равны. Математический закон выражается уравнениями (1.3) – (1.4) для изохорного и изобарного процесса. Взаимосвязь изохорного и изобарного тепловых эффектов определяется выражением: D H = D U + D nRT, (1.19) где D n – изменение числа молей газообразных веществ в реакции. Тепловой эффект может быть определен по закону Гесса методом термохимических схем. Например: C(т), О2 (г)
q2 CO(г), 1/2 O2 Тогда: q1 = q2 + q3 (1.20) Для расчета тепловых эффектов составляют термохимические уравнения, в которых рядом с символом химического соединения указывают агрегатное состояние (г – газ, ж – жидкость, т – твердое, aq – соединение или ион в растворе) и в правой части – численное значение теплового эффекта. Например: Mn(т) + 2Н+ (aq) = Mn2+ (aq) + H2(г) - 227,7 кДж. Если реакция задана в общем виде: aA + bB = cC + dD + DH, (1.21) то тепловой эффект можно определить по следующей формуле: DH = cDHС + dDHD - aDHA - bDHB = где DНi – теплота образования вещества i; DНj – теплота образования вещества j; a, b, n – стехиометрические коэффициенты в термохимическом уравнении. Теплотой образования называют тепловой эффект образования данного соединения из простых веществ в стабильном состоянии (теплота образования простых веществ принята равной нулю). Теплоты образования, определенные при стандартных условиях (Р = 1,013*105 Па = 1 атм, Т = 298 К) в расчете на 1 моль, приведены в термохимических справочниках. Если уравнения (1.6) и (1.7) применить к тепловому эффекту, то получим: (¶DU/¶Т)v = DCv; (D¶ H/¶T)p = DCp, (1.23) где DС = D HT = D H0 + где DH0 – тепловой эффект реакции в стандартных условиях; DHT – тепловой эффект при температуре Т. Уравнение (1.24) позволяет рассчитывать тепловые эффекты при любых температурах по термохимическим таблицам.
|

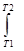 CvdT
CvdT
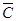 в интервале температур:
в интервале температур: CdT, (1.15)
CdT, (1.15) СO2(г)
СO2(г) q3
q3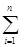 (DHini)прод. -
(DHini)прод. -  (DHjnj)исх., (1.22)
(DHjnj)исх., (1.22) (nc)прод. -
(nc)прод. -  DCpdT, (1.24)
DCpdT, (1.24)


