Уравнение Редлиха-Квонга
Уравнение Редлиха-Квонга [17, 18] имеет вид:
где P — давление, Па; T — абсолютная температура, К; V — мольный объём, м³/моль;
a и b - некоторые константы, зависящие от конкретного вещества. Уравнение состояния Редлиха-Квонга значительно проще большинства известных уравнений. Точность данного уравнения в целом соответствует точности определения состава и свойств остатка пластовых смесей [19]. Первоначально уравнение состояния Редлиха-Квонга использовали для определения термодинамических и физических свойств газовых смесей. Применение этого уравнения для расчета свойств жидких углеводородных смесей приводит к большим погрешностям [20]. В практике расчета равновесий широкую известность получилиуравнения состояния Редлиха-Квонга, Соаве, Пенга-Робинсона, Бенедикта-Вебба-Рубина, позволяющие рассчитывать равновесие жидкость-пар в однокомпонентных, бинарных и многокомпонентных системах в весьма широком интервале внешних условий. Смеси неполярных веществ обычно с удовлетворительной точностью описывают только на основе данных о чистых компонентах. Параметры уравнений для смесей при этом находят с помощью определенных комбинационных правил на основе констант, характеризующих индивидуальные вещества. В более сложных случаях необходима оценка некоторых бинарных параметров по экспериментальным данным для смесей [21]. Летучесть компонента смеси в газовой фазе рассчитывают по уравнению состояния Редлиха-Квонга, а коэффициент активности по выражению из теории регулярных растворов Гильденбранта. В это выражение входят молярный объем компонента в жидком состоянии и параметр растворимости, который вычисляют по энтальпии испарения компонента смеси [22]. Метод Чао и Сидера рекомендуется использовать в расчетах процессов стабилизации и дебутанизации насыщенного конденсата, а также сепарации природных газоконденсатных смесей при давлениях примерно до 10 МПа и температуре не ниже 263 К - чтобы расширить пределы применимости этого метода, предпринимались попытки его модификации, основанные на использовании различных модификаций уравнения состояния Редлиха-Квонга и теории жидких растворов. Робинсон и Чао коэффициент летучести компонента в газовой фазе вычисляют поуравнению состояния Редлиха-Квонга с использованием обобщенных коэффициентов Чу и Прауснитца. Для определения летучести чистого вещества подобраны эмпирические выражения, отличающиеся от выражений Чао, Сидера и Шелтона. Коэффициент активности рассчитывают с помощью уравнения Гильдебранта и Скотта, учитывающего отклонение поведения жидких растворов от поведения регулярных растворов. Особенно эффективной оказалось модификация, предложенная Соаве, которая часто дает хорошие результаты при расчетах равновесия пар-жидкость в углеводородных смесях. Это объясняется, по крайней мере частично, использованием для определения констант уравнения данных по давлениям паров чистых компонентов. В результате уравнение Соаве, надежное почти всегда при расчете констант равновесия К, обычно дает неправильные значения плотности жидкости [23]. В заключение следует отметить, что, несмотря на простоту, осуществленная Соаве модификация уравнения Редлиха-Квонга явилась очень эффективной и позволила улучшить моделирование свойств не только паровой (газовой) фазы, но и газированной жидкой фазы. И все же, свойства паровой фазы моделируются модификациями уравнения состояния Редлиха-Квонга значительно более точно, чем свойства жидкой фазы. Для точного описания фазового равновесия необходимо правильно определять свойства обеих сосуществующих фаз.
|

 (1.15)
(1.15)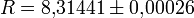 — универсальная газовая постоянная, Дж/(моль·К);
— универсальная газовая постоянная, Дж/(моль·К);


