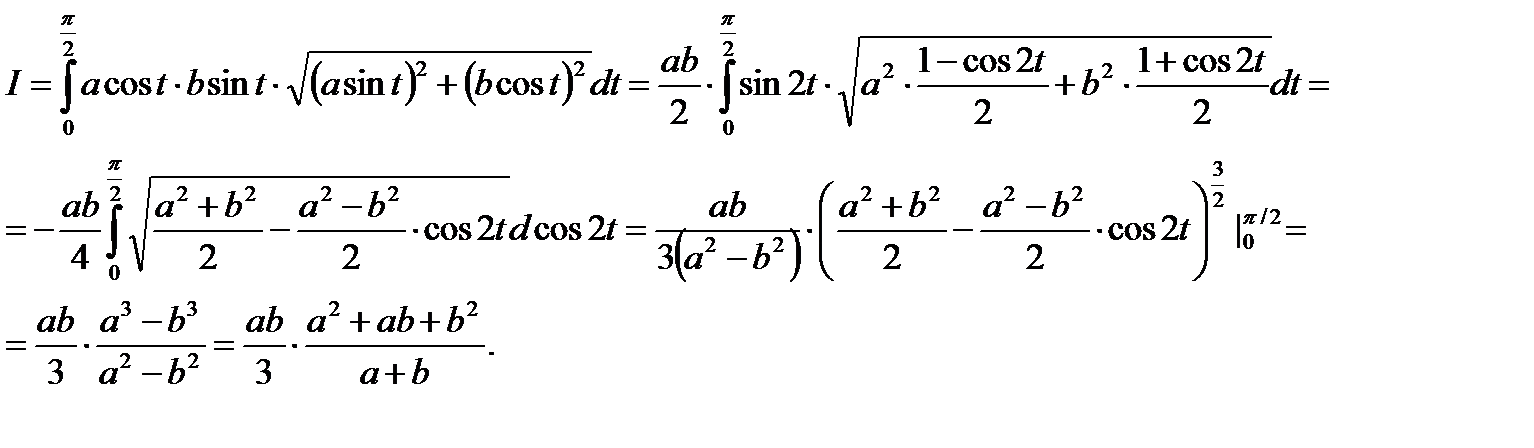Определение криволинейного интеграла первого рода. 1. Про автомобільний транспорт: Закон України від 23 лютого 2006 р
1. Про автомобільний транспорт: Закон України від 23 лютого 2006 р. № 3492-IV. 2. Про дорожній рух: Закон України від 30 червня 1993 р. № 3353-XII//Відомості Верховної Ради України. – 1993.– № 31.– с.338.. Основная и вспомогательная литература 1. Босняк М. Г. Вантажні автомобільні перевезення. Навчальний посібник для студентів спеціальності 7.100403 "Орrанiзацiя перевезенъ i управлiння на транспортi (автомобiлъний)". / М. Г. Босняк. К.: Видавиичий Дiм "Слово", 2010. 408 с. 2. Вельможин А.В. Грузовые автомобильные перевозки. Учебник для вузов. / В.А. Гудков, Л.Б. Миротин, А.В. Куликов. – М.: Горячая линия – Телеком, 2007 – 500 с. 3. Герзель В.М. Організація автомобільних перевезень, дорожні умови та безпека руху: Навч. посіб. / В.М.Герзель, М.М.Марчук, М.А.Фабрицький, О.П.Рижий; Нац. ун-т водн. гос-ва та природокорист. - Рівне: [НУВГП], 2008. - 199 с. 4. Горев А.Э. Грузовые автомобильные перевозки: учеб. Пособие для студ. высш. учеб. заведений. / А.Э. Горев. – М.: Издательский центр «Академия», 2006. -288 с. 5. Зінь Е.А. Управління автомобільним транспортом: Навч. посібник. / Е.А. Зінь. – Рівне: НУВГП, 2011. – 326 с. 6. Куликов Ю.И. Грузоведение на автомобильном транспорте: Учеб. Пособие. / Ю.И.Куликов; Тихоокеанский гос. универ-т. - М.: Академия, 2008. - 208 с.. 7. Мирошниченко Л. Автомобильные перевозки: организация и учт. / Л.Мирошниченко. - Харьков: Фактор, 2003.-522 с. 8. Пашков А.К. Пакетирование и перевозка тарноштучных грузов. / А.К.Пашков, Ю.Н.Полярин Москва: Транспорт, 2000. – 254 с. 9. Сарафанова Е.В. Грузовые автомобильные перевозки: Учеб. Пособие. / Е.В.Сарафанова, А.А.Евсеева, Б.П.Копцев. - Москва-Ростов-на-Дону: Март, 2006.- 476 с. 10. Фабрицький М.А. Організація автомобільних перевезень, дорожні умови та безпека руху: Навч. Посібник. / М.А.Фабрицький, М.М.Марчук, О.П.Рижий. - Рівне: РДТУ, 2001. – 144 с. 11.
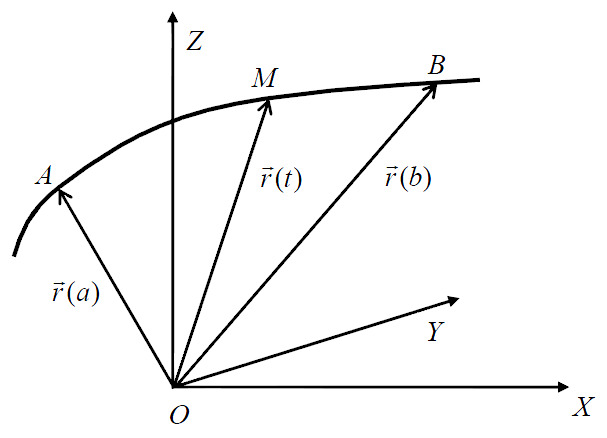
Геометрическое и физическое применение криволинейного интеграла Криволинейный интеграл первого рода Определение криволинейного интеграла первого рода. Рассмотрим в трехмерном пространстве с заданной декартовой системой координат ОXYZ некоторую кривую Г (см. рис. 1). Декартовы координаты точек кривой будем обозначать через (х, у, z).
Определение 1. Кривая, заданная уравнением
называется непрерывной кусочно-гладкой, если функции
Рис.1. К определению кривой. Пусть на кривой Г
Рис. 2. Разбиение кривой Г.
Зададим разбиение T кривой Г точками A = N o, N 1, N 2, …, Nn = B, (см. рис. 2).На каждой из дуг ∪ NkNk +1 выберем по произвольной точке Mk с координатами (ξ k, η k, ζ k) и составим интегральную сумму:
где Δ sk – длина дуги ∪ NkNk +1.
Определение 2. Криволинейным интегралом первого рода от функции
Для криволинейного интеграла по замкнутой кривой Г используется иное обозначение:
Существование криволинейного интеграла устанавливает следующая теорема:
Теорема 1. Если Г – непрерывная кусочно-гладкая кривая и функция f (M) непрерывна на ней, то криволинейный интеграл первого рода (3) от функции f (M) существует и определен однозначно.
Теорема 2. Если кривая Г задана уравнениями (1), а функция f (M) непрерывна на этой кривой, то криволинейный интеграл первого рода от функции f (M) находится по формуле
Замечание. При использовании формулы (4) следует обращать внимание на то, чтобы при изменении параметра t от а до b дифференциалы ds и dt были неотрицательными, поскольку выражение
задает элемент длины дуги, который отрицательным быть не может.
ПРИМЕР 1. Найти интеграл
Рис.3. К примеру 1. Рис.4. К примеру 2.
ПРИМЕР 2. На кривой Г, заданной параметрически уравнениями точками С уменьшением длин дуг ∪ NkNk +1 разбиения исходной кривой интегральная сумма приближается к искомой массе. В пределе получаем:
Замечание. В случае кривой на плоскости:
сохраняются определения и остаются справедливыми все теоремы, сформулированные выше. В соответствующих формулах нужно лишь убрать третью координату z (t) или ζ k. ПРИМЕР 3. Вычислить интеграл
Рис.5. К примеру 3.
Пусть для определенности a > b. Введем параметризацию дуги:
|

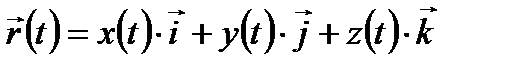 ,
,  , (1)
, (1)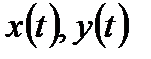 и
и 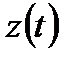 непрерывны на отрезке
непрерывны на отрезке 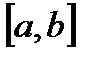 и
и 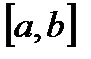 отрезок может быть разбит точками
отрезок может быть разбит точками 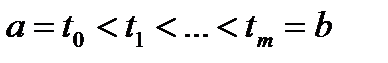 на конечное число отрезков таким образом, что на каждом из этих частичных отрезков функции
на конечное число отрезков таким образом, что на каждом из этих частичных отрезков функции  и
и 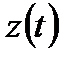 имеют непрерывные производные, не обращающиеся одновременно в
имеют непрерывные производные, не обращающиеся одновременно в  .
.
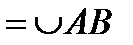 , где
, где 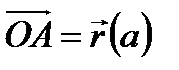 ,
, 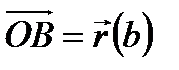 задана непрерывная функция
задана непрерывная функция 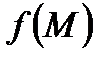 , где
, где 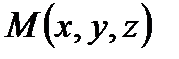 – точка на кривой.
– точка на кривой.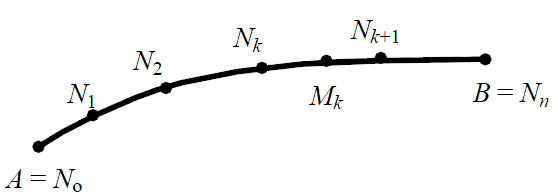

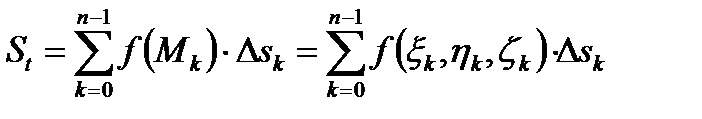 , (2)
, (2)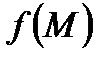 по кривой Г называется предел интегральной суммы (2) при бесконечном увеличении числа n точек деления Nk и бесконечном уменьшении длин дуг∪ NkNk +1, если этот предел существует и не зависит ни от способа разбиения T, ни от выбора точек Mk на дугах:
по кривой Г называется предел интегральной суммы (2) при бесконечном увеличении числа n точек деления Nk и бесконечном уменьшении длин дуг∪ NkNk +1, если этот предел существует и не зависит ни от способа разбиения T, ни от выбора точек Mk на дугах: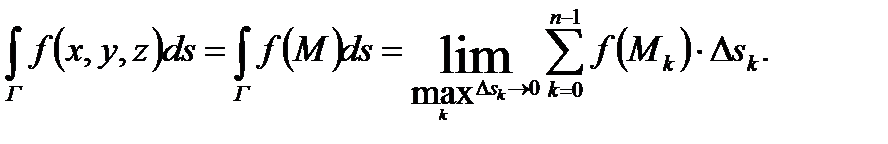 (3)
(3)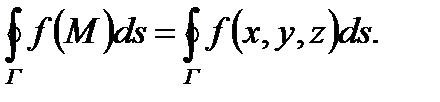
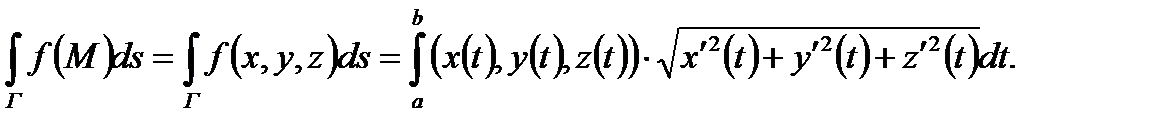 (4)
(4)
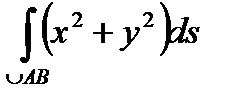 , где кривая Г – дуга окружности с центром в начале координат и радиуса 1 между точками А (0, 1) и В (1, 0) (см. рис.3). Введем на кривой Г параметризацию:
, где кривая Г – дуга окружности с центром в начале координат и радиуса 1 между точками А (0, 1) и В (1, 0) (см. рис.3). Введем на кривой Г параметризацию: 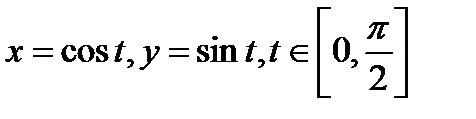 . Тогда
. Тогда 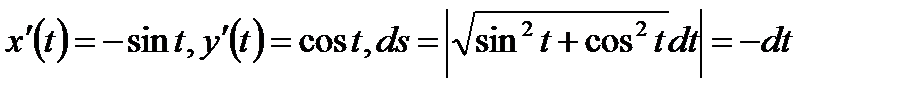 . Здесь модуль раскрывается со знаком «–» поскольку при интегрировании от точки А до точки В параметр t изменяется в интервале от π /2 до 0 и, следовательно, dt < 0. Применяя формулу (4), получим:
. Здесь модуль раскрывается со знаком «–» поскольку при интегрировании от точки А до точки В параметр t изменяется в интервале от π /2 до 0 и, следовательно, dt < 0. Применяя формулу (4), получим: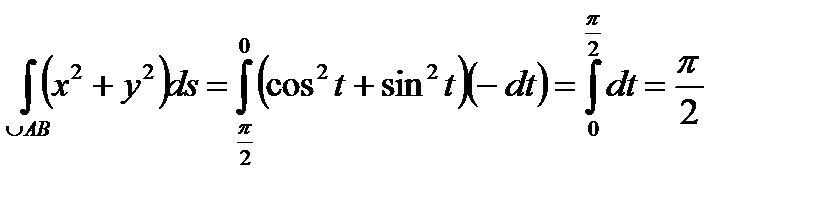
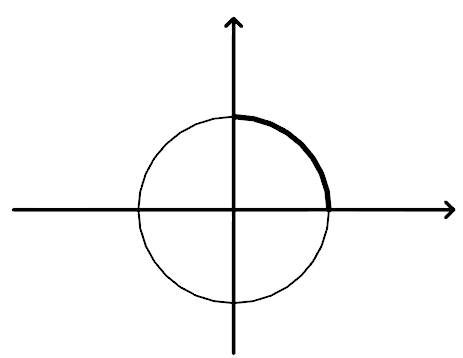

 , распределена масса с плотностью
, распределена масса с плотностью 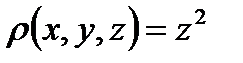 . Определить массу кривой. Кривая Г представляет собой два витка спирали (см. рис.4). Для определения ее массы воспользуемся процедурой, аналогичной применявшейся при введении понятия криволинейного интеграла. Проведем разбиение T кривой Г
. Определить массу кривой. Кривая Г представляет собой два витка спирали (см. рис.4). Для определения ее массы воспользуемся процедурой, аналогичной применявшейся при введении понятия криволинейного интеграла. Проведем разбиение T кривой Г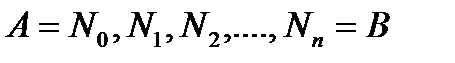 на элементарные дуги ∪ NkNk +1. На каждой дуге выберем по точке Mk и будем считать, что плотность кривой на этой дуге постоянна и равна значению ρ(Mk) плотности в точке Mk. Тогда масса элементарной дуги равна произведению плотности на длину дуги: Δ mk = ρ(Mk)·Δ sk. Масса всей кривой равна сумме масс всех элементарных дуг:
на элементарные дуги ∪ NkNk +1. На каждой дуге выберем по точке Mk и будем считать, что плотность кривой на этой дуге постоянна и равна значению ρ(Mk) плотности в точке Mk. Тогда масса элементарной дуги равна произведению плотности на длину дуги: Δ mk = ρ(Mk)·Δ sk. Масса всей кривой равна сумме масс всех элементарных дуг: 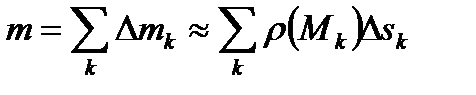 . Полученное выражение представляет собой интегральную сумму криволинейного интеграла первогорода
. Полученное выражение представляет собой интегральную сумму криволинейного интеграла первогорода 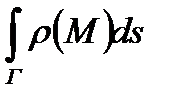 функции ρ(М) по дуге Г.
функции ρ(М) по дуге Г.
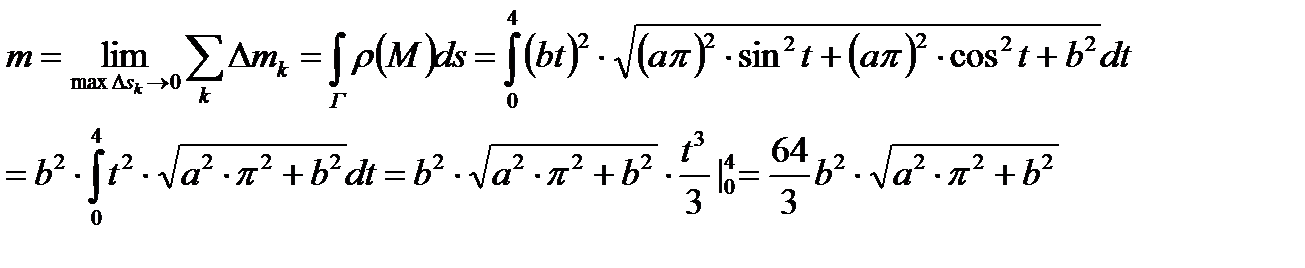
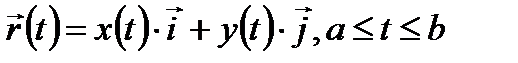 (5)
(5)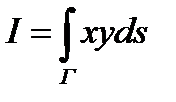 , где Г – четверть эллипса
, где Г – четверть эллипса 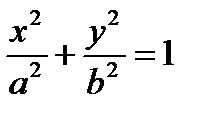 , лежащая в первом квадрате (см. рис. 5).
, лежащая в первом квадрате (см. рис. 5).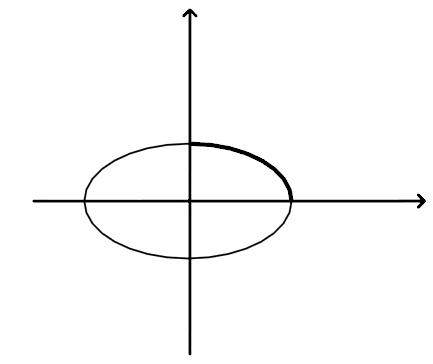
 ,
,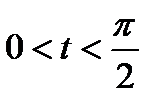 . Тогда, используя теорему 2, получаем
. Тогда, используя теорему 2, получаем