После каждого столкновения молекула непредсказуемым образом изменяет свое направление. Траектория молекулы представляет собой запутанный клубок, состоящий из отрезков прямой. Определим средний квадрат перемещения молекулы за время t.
Пусть за время t молекула испытала N соударений. Обозначим через 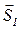 ,
,  , перемещения молекулы между последовательными соударениями. Полное перемещение за время t равно сумме перемещений
, перемещения молекулы между последовательными соударениями. Полное перемещение за время t равно сумме перемещений
 . (2)
. (2)
Проекция на координатные оси равна сумме проекций. Рассмотрим одну из них
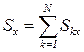 . (3)
. (3)
Найдем квадрат суммы х -проекций:
 . (4)
. (4)

 Слагаемые в правой части уравнения (4) распределены по двум группам. Одна группа – сумма квадратов каждого шага Skx. Другая - сумма всевозможных удвоенных произведений. Определим среднее значение
Слагаемые в правой части уравнения (4) распределены по двум группам. Одна группа – сумма квадратов каждого шага Skx. Другая - сумма всевозможных удвоенных произведений. Определим среднее значение  . Учтем, что в равновесном состоянии
. Учтем, что в равновесном состоянии 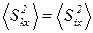 для любых пар шагов. Кроме того, из отсутствия какого-либо макроскопического течения в газе следует, что среднее значение каждого шага равно нулю
для любых пар шагов. Кроме того, из отсутствия какого-либо макроскопического течения в газе следует, что среднее значение каждого шага равно нулю  . Откуда
. Откуда
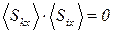 . (5)
. (5)
Таким образом, из уравнения (4), находим
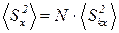 . (6)
. (6)
Длина вектора перемещения  равна сумме квадратов проекций
равна сумме квадратов проекций
 . (7)
. (7)
Сумма в правой части уравнения (7) равна квадрату средней длины свободного пробега, то есть
 . (8)
. (8)
Учтем, что  , где t - среднее время между соударениями. Оно равно
, где t - среднее время между соударениями. Оно равно  , где u0 - средне квадратичная скорость молекул. Поэтому для среднего квадрата перемещения можно записать:
, где u0 - средне квадратичная скорость молекул. Поэтому для среднего квадрата перемещения можно записать:
 . (9)
. (9)
Средний квадрат смещения оказался пропорциональным времени движения. Процесс удаления молекулы от начального положения именуют самодиффузией. Коэффициент
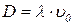 (10)
(10)
называется коэффициентом самодиффузии.

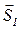 ,
,  , перемещения молекулы между последовательными соударениями. Полное перемещение за время t равно сумме перемещений
, перемещения молекулы между последовательными соударениями. Полное перемещение за время t равно сумме перемещений  . (2)
. (2) 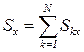 . (3)
. (3) . (4)
. (4)
 Слагаемые в правой части уравнения (4) распределены по двум группам. Одна группа – сумма квадратов каждого шага Skx. Другая - сумма всевозможных удвоенных произведений. Определим среднее значение
Слагаемые в правой части уравнения (4) распределены по двум группам. Одна группа – сумма квадратов каждого шага Skx. Другая - сумма всевозможных удвоенных произведений. Определим среднее значение  . Учтем, что в равновесном состоянии
. Учтем, что в равновесном состоянии 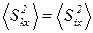 для любых пар шагов. Кроме того, из отсутствия какого-либо макроскопического течения в газе следует, что среднее значение каждого шага равно нулю
для любых пар шагов. Кроме того, из отсутствия какого-либо макроскопического течения в газе следует, что среднее значение каждого шага равно нулю  . Откуда
. Откуда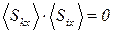 . (5)
. (5)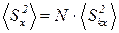 . (6)
. (6) равна сумме квадратов проекций
равна сумме квадратов проекций  . (7)
. (7)  . (8)
. (8)  , где t - среднее время между соударениями. Оно равно
, где t - среднее время между соударениями. Оно равно  , где u0 - средне квадратичная скорость молекул. Поэтому для среднего квадрата перемещения можно записать:
, где u0 - средне квадратичная скорость молекул. Поэтому для среднего квадрата перемещения можно записать: . (9)
. (9)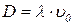 (10)
(10) 


