Диффузия броуновских частиц
Частицы малых размеров, но являющиеся макроскопическими по отношению к молекулам, помещенные в жидкость или газ, совершают беспорядочные движения. Их траектории, как и траектории молекул, представляют собой запутанные клубки, увеличивающиеся со временем в размерах. Проведем расчет среднего размера клубка броуновской частицы. Пусть частица массы M движется в вязкой среде с коэффициентом вязкости h. Движение происходит под действием непрекращающихся ударов молекул среды. Пусть сила взаимодействия молекул с частицей описывается случайной функцией f(t), где Рассмотрим величины
При фиксированной температуре средняя кинетическая энергия частицы остается постоянной, поэтому правая часть уравнения (18) не изменяется со временем. Интегрирование уравнения дает:
Броуновский клубок может быть видимым, если из одного места начинают диффузионное движение сразу огромное число частиц.
|

 – радиус-вектор частицы. В отсутствии внешних сил уравнение движения частицы можно записать в виде:
– радиус-вектор частицы. В отсутствии внешних сил уравнение движения частицы можно записать в виде:  (11)
(11)  - мгновенная скорость броуновской частицы. Проведем следующее преобразование уравнения: умножим обе части уравнения скалярно на радиус-вектор частицы. При этом получим:
- мгновенная скорость броуновской частицы. Проведем следующее преобразование уравнения: умножим обе части уравнения скалярно на радиус-вектор частицы. При этом получим:  (12)
(12) и
и  .Имеем:
.Имеем:  ®, (13)
®, (13)  (14)
(14)  (15)
(15)  (16)
(16)  являются независимыми, поэтому
являются независимыми, поэтому  и á
и á 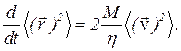 (18)
(18)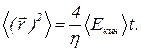 (19)
(19)  - (20)
- (20) 


